Неоднородные уравнения
Частное решение линейного неоднородного разностного уравнения (3) определяется видом его правой части, т.е. функцией
которое зависит от постоянных Для определения этих постоянных нужно воспользоваться начальными условиями В зависимости от вида правой части разностного уравнения, т.е. функцией Случай 1. Правая часть
В этом случае частное решение линейного неоднородного уравнения (3) ищется в виде полинома той же степени
где коэффициенты < 1> равенство (14) подставляется в исходное уравнение (3); < 2> в правой части полученного равенства выполняется группировка членов при одинаковых степенях < 3> приравниваются коэффициенты при одинаковых степенях независимой переменной В результате получаем систему линейных алгебраических уравнений относительно искомых коэффициентов Случай 2. Правая часть дискретного разностного уравнения имеет вид
где a - действительное число и
где коэффициенты Алгоритм вычисления неопределенных коэффициентов аналогичен алгоритму для случая 1. Случай 3. Правая часть дискретного разностного уравнения имеет вид
где a - действительное число; a является корнем характеристического уравнения (6), причем его кратность равна m. Частное решение неоднородного уравнения (3) ищется в виде
Алгоритм определения неопределенных коэффициентов Пример. Решить разностное уравнение
при начальных условиях Решение. Характеристическое уравнение
Частное решение неоднородного уравнения
коэффициент
Подставив последние равенства в исходное разностное уравнение, получаем
Общее решение однородного уравнения
общее решение линейного неоднородного уравнения
Получили систему линейных алгебраических уравнений относительно постоянных
Ответ:
|

 . После того как найдено общее решение однородного уравнения (5) и затем частное решение неоднородного уравнения (3) можно записать общее решение линейного неоднородного разностного уравнения с постоянными коэффициентами
. После того как найдено общее решение однородного уравнения (5) и затем частное решение неоднородного уравнения (3) можно записать общее решение линейного неоднородного разностного уравнения с постоянными коэффициентами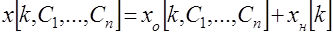 , (19)
, (19)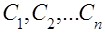 .
. ,
,  , …,
, …,  . С учетом заданных начальных условий и решения уравнения (19) получим систему линейных уравнений (алгебраических) относительно постоянных
. С учетом заданных начальных условий и решения уравнения (19) получим систему линейных уравнений (алгебраических) относительно постоянных  степени
степени  .
. . (13)
. (13) , (14)
, (14) ,,
,,  подлежат определению. Коэффициенты
подлежат определению. Коэффициенты  , (15)
, (15) не является корнем характеристического уравнения (6). В этом случае частное решение линейного неоднородного уравнения (3) ищется в виде
не является корнем характеристического уравнения (6). В этом случае частное решение линейного неоднородного уравнения (3) ищется в виде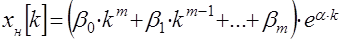 , (16)
, (16) , (17)
, (17) , (18)
, (18)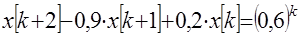 ,
, ,
,  .
. ,
, ,
, ,
, ,
,  .
. ,
, ,
, 
 ,
,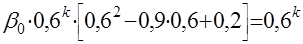 ,
,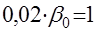 ,
,  ,
, .
. ,
, ,
,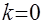 ,
,  ,
,  ;
; ,
,  ,
, .
. и
и 
 ,
,  ,
, ,
,  ,
, 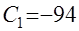 ,
,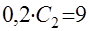 ,
, 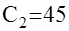 .
. .
.


