ТЕОРЕМА О КВАНТОВАНИИ
Если моменты квантования следуют достаточно часто, то при квантовании непрерывного сигнала потери информации незначительны, и наоборот. В качестве примера можно привести квантование синусоиды.
Квантование синусоиды осуществляется два раза за период. Поэтому синусоида неотличима от нулевого сигнала, если частота синусоидального сигнала равна половине частоты квантования. Для квантования непрерывного сигнала необходимо знать, при каких условиях непрерывный (аналоговый) сигнал однозначно представляется соответствующими дискретными функциями (своими дискретами). Следующая теорема определяет условия квантования периодической функции. ТЕОРЕМА ШЕНОНА.
где Доказательство. Пусть
Введем в рассмотрение функцию
разложение которой в ряд Фурье имеет вид
где Предположим теперь, что дискреты
Отсюда следует, что квантованный сигнал
Таким образом, преобразование Фурье непрерывного сигнала однозначно представляется функцией
Для доказательства справедливости ( 1 ) заметим, что она может быть получена из ( 2 ) и ( 7 )
с учетом ( 5 ) и ( 6 ). Меняя порядок интегрирования и суммирования, имеем
Откуда получаем (1), т.к.
|



 , однозначно представляется своими значениями в равноотстоящих точках, если частота квантования больше
, однозначно представляется своими значениями в равноотстоящих точках, если частота квантования больше  . При этом непрерывный сигнал может быть получен из дискретного по интерполяционной формуле
. При этом непрерывный сигнал может быть получен из дискретного по интерполяционной формуле , ( 1 )
, ( 1 ) – период квантования;
– период квантования;  - угловая частота квантования, ее размерность [1/с] (радиан в секунду).
- угловая частота квантования, ее размерность [1/с] (радиан в секунду). – непрерывный сигнал;
– непрерывный сигнал;  - его преобразование по Фурье
- его преобразование по Фурье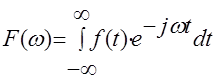 , ( 2 )
, ( 2 ) ( 3 )
( 3 )
 , ( 4 )
, ( 4 ) , ( 5 )
, ( 5 ) .
. можно рассматривать как коэффициенты ряда Фурье для периодической функции
можно рассматривать как коэффициенты ряда Фурье для периодической функции  . (Это проверяется непосредственными вычислениями). Тогда, используя определения коэффициентов Фурье и выражения ( 3 ) и ( 4 ), можно показать, что
. (Это проверяется непосредственными вычислениями). Тогда, используя определения коэффициентов Фурье и выражения ( 3 ) и ( 4 ), можно показать, что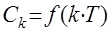 . ( 6 )
. ( 6 )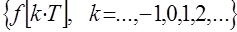 однозначно определяет функцию
однозначно определяет функцию  равна нулю вне интервала
равна нулю вне интервала  . Если
. Если  , то
, то . (7)
. (7)

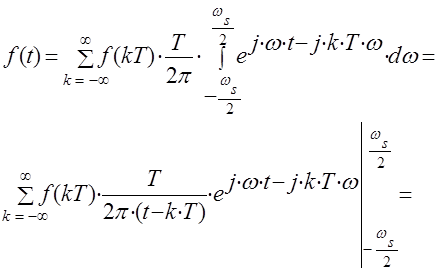
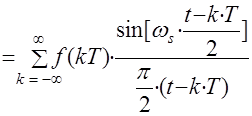 .
.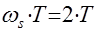 .
.


