Дискретность сигналов в цифровых системах обусловлена их квантованием по уровню и по времени. В противоположность непрерывным сигналам, которые описываются непрерывными функциями времени, дискретные сигналы могут принимать лишь дискретные значения в дискретные моменты времени.
Мы будем рассматривать сигналы, дискретные во временной области. Они представляют собой последовательности импульсов, появляющиеся в определенные моменты времени. Обычно дискретный сигнал получается в результате периодического прерывания непрерывного сигнала с постоянным периодом (тактом).
В цифровых системах управления обычно применяется лишь амплитудная модуляция импульсов, причем в основном тот ее вариант, при котором высота импульса пропорциональна текущему значению непрерывного сигнала, ширина постоянна, а интервалы между импульсами одинаковы и равны такту квантования.
Рисунок иллюстрирует принцип получения последовательности импульсов, основанный на прохождении непрерывного сигнала  через ключ, который периодически с тактом квантования
через ключ, который периодически с тактом квантования  , замыкается на время
, замыкается на время  .
.
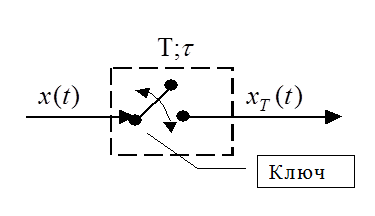

Если длительность импульса  существенно меньше периода квантования
существенно меньше периода квантования  ,
,  , или
, или  , то последовательность импульсов
, то последовательность импульсов  можно приближенно рассматривать как дискретный сигнал
можно приближенно рассматривать как дискретный сигнал  -дискретную функцию, вид которой показан на рисунке
-дискретную функцию, вид которой показан на рисунке
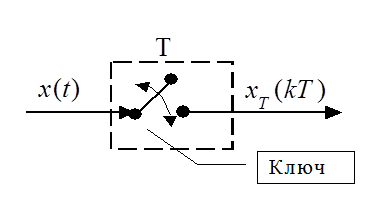
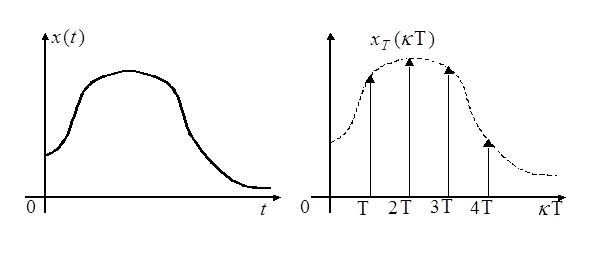
В этом случае ключ действует как идеальный квантующий элемент, и величины  равны мгновенным значениям сигнала (амплитуд).
равны мгновенным значениям сигнала (амплитуд).
Модулированная по амплитуде дискретная функция  , которая получается путем квантования по времени непрерывного сигнала
, которая получается путем квантования по времени непрерывного сигнала  с постоянным тактом
с постоянным тактом  математически описывается выражением
математически описывается выражением
 ,
, 
Наряду с функциями, определенными на всей вещественной оси  , можно рассматривать функции, которые определены только в некоторых точках
, можно рассматривать функции, которые определены только в некоторых точках  Такие функции называются дискретными (решетчатыми).
Такие функции называются дискретными (решетчатыми).
Мы будем рассматривать функции, определенные только в равноотстоящих точках  , где
, где  - любое целое число,
- любое целое число,  - постоянная, называемая периодом дискретности. Дискретные функции принято обозначать
- постоянная, называемая периодом дискретности. Дискретные функции принято обозначать  .
.
Любой непрерывной функции  можно поставить в соответствие некоторое множество решетчатых функций, если представить аргумент
можно поставить в соответствие некоторое множество решетчатых функций, если представить аргумент  в виде
в виде 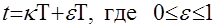
При каждом фиксированном значении переменной  функцию
функцию  можно рассматривать как решетчатую функцию, определенную в точках
можно рассматривать как решетчатую функцию, определенную в точках  . Такие функции называются смещенными дискретными (решетчатыми) функциями. Эти функции будем обозначать
. Такие функции называются смещенными дискретными (решетчатыми) функциями. Эти функции будем обозначать 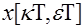 . Изменяя переменную
. Изменяя переменную  от 0 до 1, можно получить множество смещенных решетчатых функций
от 0 до 1, можно получить множество смещенных решетчатых функций 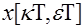 , соответствующих данной непрерывной функции
, соответствующих данной непрерывной функции  . Благодаря непрерывности функции
. Благодаря непрерывности функции  , функция
, функция 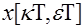 является непрерывной по аргументу
является непрерывной по аргументу  .
.
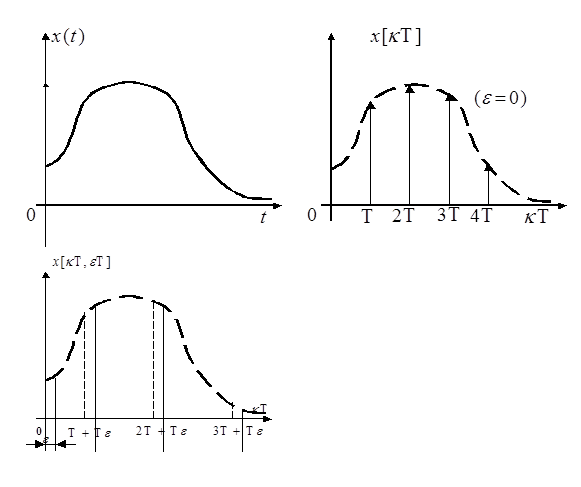
Функция  является функцией одного аргумента
является функцией одного аргумента  при фиксированном значении
при фиксированном значении  . Поэтому в дальнейшем постоянную
. Поэтому в дальнейшем постоянную  в обозначении дискретной функции будем опускать и дискретную функцию будем обозначать как
в обозначении дискретной функции будем опускать и дискретную функцию будем обозначать как  Аналогично для смещенной дискретной функции
Аналогично для смещенной дискретной функции 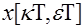 -функция двух переменных
-функция двух переменных  и
и 
 .
.

 через ключ, который периодически с тактом квантования
через ключ, который периодически с тактом квантования  , замыкается на время
, замыкается на время  .
.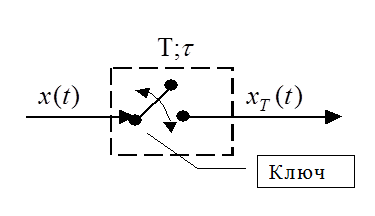

 ,
,  , или
, или  , то последовательность импульсов
, то последовательность импульсов  можно приближенно рассматривать как дискретный сигнал
можно приближенно рассматривать как дискретный сигнал  -дискретную функцию, вид которой показан на рисунке
-дискретную функцию, вид которой показан на рисунке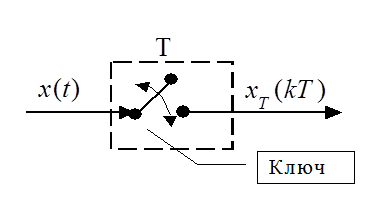
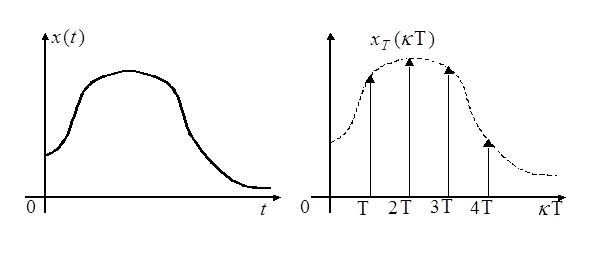
 ,
, 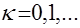
 , можно рассматривать функции, которые определены только в некоторых точках
, можно рассматривать функции, которые определены только в некоторых точках  Такие функции называются дискретными (решетчатыми).
Такие функции называются дискретными (решетчатыми). , где
, где  - любое целое число,
- любое целое число,  .
.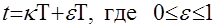
 функцию
функцию  можно рассматривать как решетчатую функцию, определенную в точках
можно рассматривать как решетчатую функцию, определенную в точках  . Такие функции называются смещенными дискретными (решетчатыми) функциями. Эти функции будем обозначать
. Такие функции называются смещенными дискретными (решетчатыми) функциями. Эти функции будем обозначать 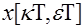 . Изменяя переменную
. Изменяя переменную 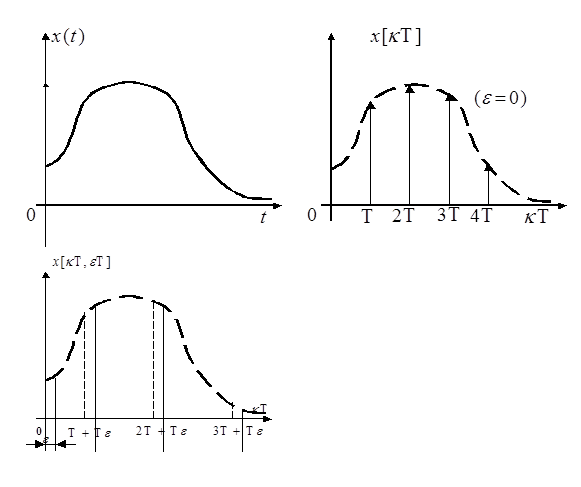
 Аналогично для смещенной дискретной функции
Аналогично для смещенной дискретной функции  и
и  .
.


