Дискретное преобразование Фурье. Это преобразование позволяет распространить частотные методы исследования, разработанные для непрерывных систем автоматического управления
Это преобразование позволяет распространить частотные методы исследования, разработанные для непрерывных систем автоматического управления, на дискретные системы. Пусть абсцисса абсолютной сходимости дискретного преобразования Лапласа (1) функции
Эта формула прямого преобразования дискретного Фурье. Обратное дискретное преобразование Фурье определяется по формуле
Эта формула получается из формулы обратного дискретного преобразования Лапласа при Функцию Связь между непрерывным преобразованием Фурье
В частности при
Выражение (36) связывает преобразование Фурье
где Из формул (36) и (38) следует теорема Котельникова, которая устанавливает связь между непрерывными и дискретными функциями.
|
отрицательна 
. Тогда изображение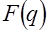 
существует и является аналитической функцией в правой полуплоскости 
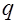и на мнимой оси. Пологая в формуле (1) 
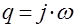, получим
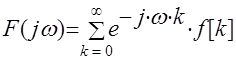. (34)
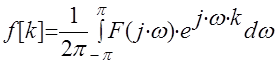. (35)
.
в этом случае можно назвать спектральной характеристической дискретной функцией 
для непрерывной функции 
и соответствующей ей дискретной функции 
, имеющей дискретное преобразование Фурье 
(36)
.
формула (36) принимает вид
. (37)
соответствующей дискретной функцией 
, (38)
.
