Линейным разностным уравнением называется соотношение вида
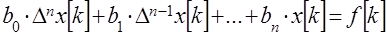 , (1)
, (1)
где 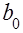 , …,
, …, 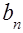 – постоянные числа;
– постоянные числа;  – заданная дискретная функция. Разностное уравнение устанавливает связь между дискретной функцией
– заданная дискретная функция. Разностное уравнение устанавливает связь между дискретной функцией  и ее разностями. С помощью формулы
и ее разностями. С помощью формулы
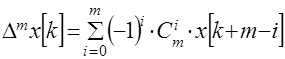 (2)
(2)
уравнение (1) можно преобразовать к виду
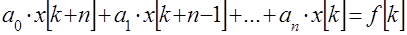 . (3)
. (3)
При этом коэффициенты 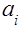 связаны с коэффициентами
связаны с коэффициентами 
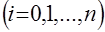 соотношением
соотношением
 . (4)
. (4)
Число  в уравнении (3) называется периодом разностного уравнения. Число
в уравнении (3) называется периодом разностного уравнения. Число  в равенстве (1) и (3) могут не совпадать, но порядок разностного уравнения (1) определяется после его преобразования к уравнению вида (3). Таким образом, порядок разностного уравнения (1) может отличаться от порядка старшей разности.
в равенстве (1) и (3) могут не совпадать, но порядок разностного уравнения (1) определяется после его преобразования к уравнению вида (3). Таким образом, порядок разностного уравнения (1) может отличаться от порядка старшей разности.
Дискретная функция  , которая обращает разностное уравнение в тождество, называется решением разностного уравнения. Далее мы будем рассматривать разностные уравнения, записанные в виде (3).
, которая обращает разностное уравнение в тождество, называется решением разностного уравнения. Далее мы будем рассматривать разностные уравнения, записанные в виде (3).
Разностное уравнение вида (3) называется неоднородным разностным уравнением порядка  . Если
. Если 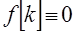 , то уравнение (3) принимает вид
, то уравнение (3) принимает вид
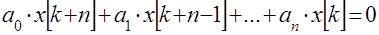 (5)
(5)
и называется однородным разностным уравнением.
Пример. Определить порядок разностного уравнения
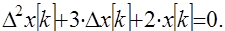
Решение. Отметим, что исходное уравнение – однородное.
 ,
,
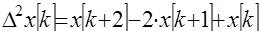 .
.
Подставим это равенство в исходное уравнение
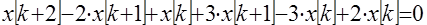 ,
,
 .
.
Замена переменной  дает
дает
 .
.
Следовательно, порядок исходного разностного уравнения равен единице.

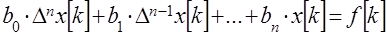 , (1)
, (1)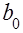 , …,
, …, 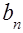 – постоянные числа;
– постоянные числа;  – заданная дискретная функция. Разностное уравнение устанавливает связь между дискретной функцией
– заданная дискретная функция. Разностное уравнение устанавливает связь между дискретной функцией  и ее разностями. С помощью формулы
и ее разностями. С помощью формулы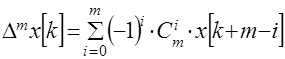 (2)
(2)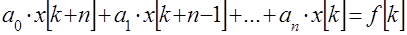 . (3)
. (3)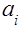 связаны с коэффициентами
связаны с коэффициентами 
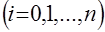 соотношением
соотношением . (4)
. (4) в уравнении (3) называется периодом разностного уравнения. Число
в уравнении (3) называется периодом разностного уравнения. Число 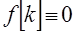 , то уравнение (3) принимает вид
, то уравнение (3) принимает вид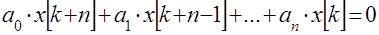 (5)
(5)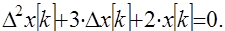
 ,
,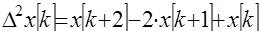 .
.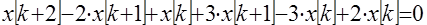 ,
, .
. дает
дает .
.


