Для исследования дискретных систем автоматического управления используется дискретное преобразование Лапласа, которое определяется формулой
 , (1)
, (1)
где  ,
, 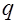 - комплексная переменная.
- комплексная переменная.
Дискретное преобразование Лапласа устанавливает связь между дискретной функцией действительного переменного  и функцией комплексного переменного
и функцией комплексного переменного 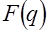 .
.
Для смещённой дискретной функции  дискретное преобразование определяется следующим образом
дискретное преобразование определяется следующим образом
 . (2)
. (2)
В задачах исследования цифровых систем автоматического управления используют не дискретное преобразование Лапласа, определяемого формулами (1) и (2), а так называемое  -преобразование, которое определяется формулами, аналогичными (1) и (2), но в которых введена новая переменная
-преобразование, которое определяется формулами, аналогичными (1) и (2), но в которых введена новая переменная 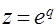 . Тогда вместо равенств (1) и (2) получаем
. Тогда вместо равенств (1) и (2) получаем
 (3)
(3)
и
 . (4)
. (4)
Если известно изображение 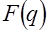 некоторой дискретной функции
некоторой дискретной функции  , то соответствующее изображение
, то соответствующее изображение 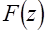 может быть найдено с помощью замены комплексной переменной
может быть найдено с помощью замены комплексной переменной 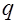 по формуле
по формуле  .
.
Таким образом, принципиальной разницы между дискретным преобразованием Лапласа и  - преобразованием не существует. Все свойства
- преобразованием не существует. Все свойства  - преобразования могут быть получены из соответствующих свойств дискретного преобразования Лапласа.
- преобразования могут быть получены из соответствующих свойств дискретного преобразования Лапласа.
Здесь следует отметить, что ряд (1) сходится абсолютно в каждой точке полуплоскости  и расходится в полуплоскости
и расходится в полуплоскости  , где
, где
 .
.
Величина  называется абсциссой абсолютной сходимости дискретного преобразования Лапласа. Таким образом, область сходимости дискретного преобразования Лапласа это полуплоскость, расположенная справа от прямой
называется абсциссой абсолютной сходимости дискретного преобразования Лапласа. Таким образом, область сходимости дискретного преобразования Лапласа это полуплоскость, расположенная справа от прямой 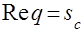
По аналогии с непрерывным преобразованием Лапласа функцию  , которая равно нулю при
, которая равно нулю при  и удовлетворяет при
и удовлетворяет при 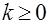 условию
условию
 (5)
(5)
будем называть оригиналом. В равенстве (5)  и
и  – некоторые постоянные величины. Величина
– некоторые постоянные величины. Величина  называется показателем роста дискретной функции
называется показателем роста дискретной функции  .
.
Функция 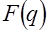 – называется изображением дискретной функции
– называется изображением дискретной функции  . Непосредственно из определения дискретного преобразования Лапласа (формула (1)) следует, что функция
. Непосредственно из определения дискретного преобразования Лапласа (формула (1)) следует, что функция 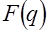 является периодической вдоль мнимой оси плоскости
является периодической вдоль мнимой оси плоскости 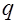 с периодом
с периодом  . Действительно
. Действительно
 ,
,
где  – любое целое число. Поэтому все свойства функции
– любое целое число. Поэтому все свойства функции 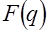 рассматриваются в любой полосе шириной
рассматриваются в любой полосе шириной  :
:  .
.
Наиболее удобной для этой цели является полоса 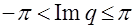 , симметричная относительно действительной оси. Эта полоса называется основной полосой.
, симметричная относительно действительной оси. Эта полоса называется основной полосой.
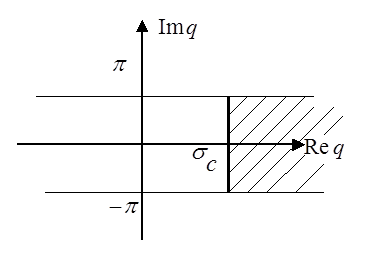
Дискретное преобразование Лапласа определяет аналитическую функцию 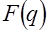 в основной полосе за исключением конечного числа особых точек. (Далее это, как правило, полюсы функции
в основной полосе за исключением конечного числа особых точек. (Далее это, как правило, полюсы функции 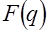 ).
).
Если все особые точки функции 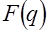 определены в основной полосе
определены в основной полосе
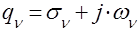 ,
,  ,
,
то все остальные полюсы (особые точки) определяются с помощью равенства
 ,
,  ,
, 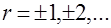 .
.
Рассмотрим, как связаны между собой области определения дискретного преобразования Лапласа в плоскости комплексной переменной 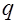 и
и  - преобразования в плоскости комплексной переменной
- преобразования в плоскости комплексной переменной  .
.
Преобразование комплексной переменной 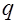 по формуле
по формуле 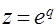 переводит основную полосу
переводит основную полосу 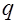 на всю расширенную плоскость комплексной переменной
на всю расширенную плоскость комплексной переменной  . При этом отрезок мнимой оси
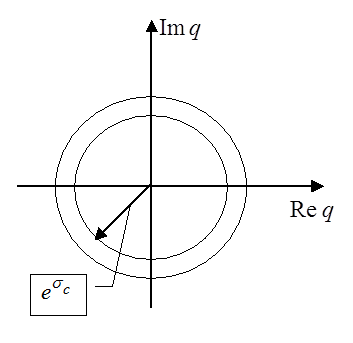
. При этом отрезок мнимой оси  отображается в окружность единичного радиуса
отображается в окружность единичного радиуса 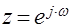 ,
,  . Левая полоса
. Левая полоса 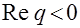 комплексной плоскости
комплексной плоскости 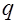 отображается во внутренность единичного круга
отображается во внутренность единичного круга  плоскости
плоскости  , а правая полоса
, а правая полоса 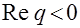 - во внешность этого круга.
- во внешность этого круга.
Функция 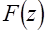 , определяемая по формуле (3), является аналитической в области
, определяемая по формуле (3), является аналитической в области  , т.е. во внешности круга
, т.е. во внешности круга  ,
,  ,
,
а после построения аналитического продолжения – во всей расширенной плоскости переменной  , за исключением конечного числа особых точек.
, за исключением конечного числа особых точек.
Особые точки
 ,
, 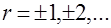
изображения 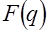 при отображении с помощью функции
при отображении с помощью функции 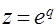 перейдут в точки
перейдут в точки
 ,
,  ,
,
лежащие внутри круга
 ;
;  .
.
Обратное дискретное преобразование Лапласа определяет дискретную функцию  по заданному изображению
по заданному изображению 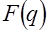
 ,
, 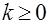 , (7)
, (7)
где 
 – абсцисса абсолютной сходимости.
– абсцисса абсолютной сходимости.
Для смещенной дискретной функции
 . (8)
. (8)
Вычисление оригиналов  можно производить и по формуле обратного
можно производить и по формуле обратного  -преобразования, которая может быть получена из формулы (7) путем замены переменной
-преобразования, которая может быть получена из формулы (7) путем замены переменной 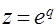
 , (9)
, (9)
где интегрирование производится по окружности 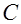 радиуса
радиуса  , контур
, контур  обходится в положительном направлении.
обходится в положительном направлении.
Для смещенных функций имеем
 . (10)
. (10)
Принимая во внимание, что функция 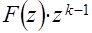 является аналитической вне окружности
является аналитической вне окружности 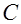 и на самой окружности, можно применить теорему о вычетах, согласно которой
и на самой окружности, можно применить теорему о вычетах, согласно которой
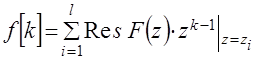 , (11)
, (11)
где  – полюс функции
– полюс функции 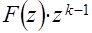 , лежащий внутри окружности
, лежащий внутри окружности 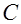 . Вычет в простом полюсе
. Вычет в простом полюсе
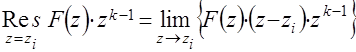 , (12)
, (12)
Вычет в полюсе кратности 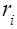
 . (13)
. (13)

 , (1)
, (1) ,
, 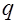 - комплексная переменная.
- комплексная переменная. и функцией комплексного переменного
и функцией комплексного переменного 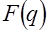 .
. дискретное преобразование определяется следующим образом
дискретное преобразование определяется следующим образом . (2)
. (2) -преобразование, которое определяется формулами, аналогичными (1) и (2), но в которых введена новая переменная
-преобразование, которое определяется формулами, аналогичными (1) и (2), но в которых введена новая переменная 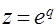 . Тогда вместо равенств (1) и (2) получаем
. Тогда вместо равенств (1) и (2) получаем (3)
(3) . (4)
. (4)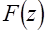 может быть найдено с помощью замены комплексной переменной
может быть найдено с помощью замены комплексной переменной  .
. и расходится в полуплоскости
и расходится в полуплоскости  , где
, где .
. называется абсциссой абсолютной сходимости дискретного преобразования Лапласа. Таким образом, область сходимости дискретного преобразования Лапласа это полуплоскость, расположенная справа от прямой
называется абсциссой абсолютной сходимости дискретного преобразования Лапласа. Таким образом, область сходимости дискретного преобразования Лапласа это полуплоскость, расположенная справа от прямой 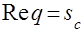
 и удовлетворяет при
и удовлетворяет при 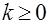 условию
условию (5)
(5) и
и  – некоторые постоянные величины. Величина
– некоторые постоянные величины. Величина  . Действительно
. Действительно ,
, – любое целое число. Поэтому все свойства функции
– любое целое число. Поэтому все свойства функции  .
.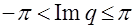 , симметричная относительно действительной оси. Эта полоса называется основной полосой.
, симметричная относительно действительной оси. Эта полоса называется основной полосой.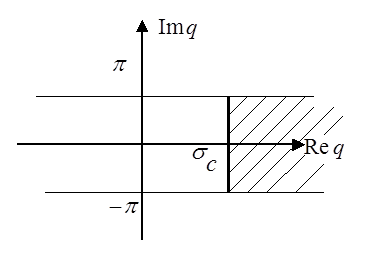
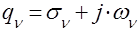 ,
,  ,
, ,
,  ,
, 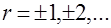 .
. .
. отображается в окружность единичного радиуса
отображается в окружность единичного радиуса 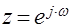 ,
, 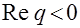 комплексной плоскости
комплексной плоскости  плоскости
плоскости  , т.е. во внешности круга
, т.е. во внешности круга  ,
, 
 ,
,  ,
,  ,
, ;
;  ,
, 
 . (8)
. (8) , (9)
, (9)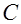 радиуса
радиуса  , контур
, контур  обходится в положительном направлении.
обходится в положительном направлении. . (10)
. (10)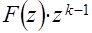 является аналитической вне окружности
является аналитической вне окружности 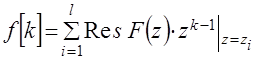 , (11)
, (11) – полюс функции
– полюс функции 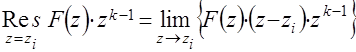 , (12)
, (12)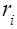
 . (13)
. (13)


