Конус. Теорема Фаркаша - Минковского
Рис. 3.8. Определение 3.8. Пусть К –выпуклый конус, тогда множество К*={y / < x, y> ³ 0, " xÎ K, yÎ En} называется сопряженным конусом.
К* В ' уÎ K* не превосходит p/2. На рисунке 3.9 К состоит из векторов угла Ð АОВ, К* О состоит из векторов угла Ð А'ОВ'. Из Рис. 3.9. рисунка видно, что Ð А'ОВ=Ð АОВ' = p /2. Лемма 3.1. Сопряженный конус является замкнутым выпуклым конусом. Доказательство. Пусть у Î K*, l > 0, тогда для любого х Î K выполняется < х, у> ³ 0, откуда < х, lу> ³ 0, следовательно lу Î K* и aÎ [0, 1]. Для любогох Î K< х, у> ³ 0, < х, z> ³ 0, поэтому< х, (1-a)y + az > ³ 0, откуда следует выпуклость K*. Остается доказать, что K* замкнутое множество. Пусть у – предельная точка множества K*, тогда в K* существует последовательность {yk}, для которой yk у. Для членов этой последовательности< yk, х> ³ 0 для любого хÎ K, т. е. Î K*. Таким образом, лемма доказана. Лемма 3.2. Если К – выпуклый конус, то К* =( Доказательство. Пусть К= Покажем справедливость обратного включения. Пусть уÎ К *, или < х, у> ³ 0, " х Î К. Так как предельный переход не меняет знака неравенства, то < х, у> ³ 0 будет справедливо и для всех х Î Геометрическая иллюстрация двойственных конусов дает возможность предполагать, что двойственный к двойственному конусу есть исходный. Этот факт доказывает следующая теорема двойственности. Теорема 3.11. (Теорема двойственности). Пусть К выпуклый конус, тогда (К*)*= Доказательство. Пусть хÎ Докажем, что (К*)*\ Положим С' = -С, тогда для всех хÎ < c’, x> < < c’, v>. (3.31) Подставим х=0nÎ Так как vÎ. (К*)*, тоиз предыдущего неравенства следует, что С' Ï К*. C другой стороны, если хÎ l < c’, x> > < c’, v> для " l > 0, хÎ Это возможно лишь в том случае, когда < c’, x> > 0 для всякого хÎ Следствие 3.3. Если К замкнутый конус, то (К*)*= К. Определение 3.9. Пусть аi (i= К={х / x= Обозначим А=(а1, а2, …, аm), l=(l1, l2, …, l m).т, тогда для конуса К можно записать К={x/x=Al, li³ 0m, хÎ Еn }. На рисунке 3.10 приведен пример многогранного конуса К. Он состоит из всех векторов, лежащих между векторами а1 и а3. Вектор х можно представить в виде х= l1а1+0а2+ l3а3, где li, l3³ 0.
Рис.3.10 Лемма 3.3. Многогранный конус является выпуклым конусом. Доказательство. Надо доказать, что К конус и что К выпуклое множество. Действительно, если х Î К, т. е. x= Следовательно, lх Î К, К – конус. Пусть х, у Î К, a Î [0, 1 ], тогда x= z=(1-a)х +ay = Вектор хÎ К может иметь не единственное представление через аi , i= Лемма 3.4. Для любой точки х Î К, К - многогранный конус, существует её представление через систему линейно независимых векторов аi, i Î w, т.е. x= где w = {I / i= 1, 2,..., m, li³ 0}. Если аi, i Î w - система линейно независимых векторов, то получим требуемое. Иначе найдутся такие ai, i Î w, не все равные нулю, что 0m= Умножая равенство (3.33) на р ³ 0 и складывая с разложением (3.32), получим x= Не ограничивая общности можно считать, что среди ai есть отрицательные числа. Если их нет, то в разложении (3.33) знаки ai можно поменять на противоположные. Начнем увеличивать значение р от 0 до момента, когда некоторые li + рai обратятся в 0. Это произойдет при p= min (-li/ai), i Î w, ai< 0. Удаляем из w все те i, для которых li + рai =0. Таким образом, число элементов в разложении вектора х (3.32), уменьшилось по крайней мере на 1. Если векторы аi , i Î w вновь линейно зависимы, то описанную процедуру сокращения числа элементов повторяем. В силу конечности m придем к разложению вектора х по системе линейно независимых векторов. Следствие 3.4. Пусть W ={ w }-множество всех таких подмножеств wÌ {1, 2, …, m}, что система векторов аi, i Î w, линейно независима, тогда К = È К(w), где wÎ W К(w) = { x / x= Лемма 3.5. Пусть система векторов аi , i Î w, линейно независима, тогда конус К(w) замкнут. Доказательство. Обозначим Аw = (аi), i Î w, т.е. Аw матрица, столбцами которой являются векторы аi , i Î w. Пусть хk Î К(w), тогда хk = Аw lk , где вектор lk в этомразложении единственный. Умножая обе части этого выражения слева на АТw , получим АТw хk = АТw Аw lk (3.35) Так как АТw Аw не вырождена, то lk = (АТw Аw) -1 АТw хk (3.36)
Значит Теорема 3.12. Многогранный конус К является замкнутым выпуклым конусом. Доказательство. По лемме 3.3. конус есть выпуклый конус. Так как объединение конечного числа замкнутых множеств есть множество замкнутое, то из следствия 3.4 и леммы 3.5. получаем, что К также замкнутое множество. Теорема 3 13. (Фаркаша – Минковского). Пусть конус К={х / хÎ Еn, ATх³ 0n }, тогда сопряженный конус К* равен Доказательство. По теореме 3.12
= { x/xÎ En, < AT x, l> ³ 0, " l ³ 0m } ( 3.38) В силу произвольности l³ 0m , получаем
Применяя теорему 3.11 получаем Следствие 3.6. Пусть х, bÎ Еn, uÎ Еm, B – матрица размерности m × n. Если < b, x> ³ 0 для всех х, удовлетворяющих системе Bх³ 0m, то система BTu=b разрешима при u ³ 0m. Доказательство. Положим в теореме 3.13 AT=В, тогда получаем, что < b, x> ³ 0 для всех хÎ К, т. е. bÎ K*. B = Au = BTu. Следствие 3.7. Для любой матрицы B и любого вектора v имеет место следующая альтернатива: либо имеет решение система (3.39)
< b, x> < 0, (3.39) либо имеет неотрицательное решение система (3.40)
u ³ 0 (3.40) Доказательство. Также, как и выше, положим АТ = В. Из первой системы следует, что bÏ K*, т.е. не может быть представлено в виде b=BTu, u ³ 0m. И наоборот, если система BTu=b разрешима при u ³ 0m, то bÎ K*, но тогда < b, x> ³ 0для любого хÎ К, но тогда первая система не разрешима.
|

 Определение 3.6. Множество КÌ Еn называется конусом, если из справедливости хÎ К следует справедливость lхÎ К для любого l> 0.
Определение 3.6. Множество КÌ Еn называется конусом, если из справедливости хÎ К следует справедливость lхÎ К для любого l> 0.



 К1 Определение 3.7. Выпуклым конусом называется конус, который одновременно
К1 Определение 3.7. Выпуклым конусом называется конус, который одновременно
 K2 является выпуклым множеством. На рисунке 3.8. множества К1 и К2 являются выпуклыми конусами. Однако К1 È К2 хотя и является конусом, но уже не являетсявыпуклым.
K2 является выпуклым множеством. На рисунке 3.8. множества К1 и К2 являются выпуклыми конусами. Однако К1 È К2 хотя и является конусом, но уже не являетсявыпуклым.



 А В Геометрически это определение означает,
А В Геометрически это определение означает,

 А' К что угол между любыми векторами xÎ K и
А' К что угол между любыми векторами xÎ K и )*.
)*. ) векторы из пространства Еn. Многогранным конусом К будем называть множество вида
) векторы из пространства Еn. Многогранным конусом К будем называть множество вида li аi , li³ 0, (i=
li аi , li³ 0, (i=  . а3
. а3


 l3 а2 х
l3 а2 х а1
а1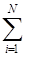 lli аi, где l li³ 0, i=
lli аi, где l li³ 0, i=  Так на рисунке 3.10 вектор х выражен через а1 и а3 Его можно также выразить через а1 и а2. Число таких представлений может быть сколь угодно велико. Из этого множества представлений выделим следующие.
Так на рисунке 3.10 вектор х выражен через а1 и а3 Его можно также выразить через а1 и а2. Число таких представлений может быть сколь угодно велико. Из этого множества представлений выделим следующие. li аi , (3.32)
li аi , (3.32) Если хk
Если хk  , то lk впредыдущем равенстве стремится к
, то lk впредыдущем равенстве стремится к = (АТw Аw) -1 АТw
= (АТw Аw) -1 АТw  (3.37)
(3.37)
 = {у / уÎ Еn , у=Al, l ³ 0n, }
= {у / уÎ Еn , у=Al, l ³ 0n, } Bx ³ 0m
Bx ³ 0m BTu=b
BTu=b


