Угловые точки выпуклого множества
Определение 3.5. Точка ZÎ Х называется угловой (крайней) точкой, если на множестве Х она не может быть представлена в виде выпуклой комбинации каких-либо точек х и у (для х¹ у) из Х: z(a)¹ (1-a)x+ay Теорема 3.10. Любая точка замкнутого выпуклого и ограниченного множества Х может быть представлена в виде выпуклой комбинации конечного числа угловых точек этого множества. Доказательство. Теорема доказывается методом математической индукции. Рассмотрим пространство Еn, содержащее множество Х. Пусть при n =1 Х является некоторым отрезком [х1, х2]. В нем х1, х2- угловые точки. Любая точка xÎ [х1, х2] может быть представлена в виде х = a1x1 + a2 х2, (3.20) где a2 = 1 - a1, a1=(х-х1 )/(х1 – х2). Пусть для пространства Еn-1 теорема верна. Покажем, что она верна и для пространства Еn. Итак, пусть х0 Î Х Ì Еn. Рассмотрим два случая. 1. Пусть х0 – граничная точка множества Х. Построим опорную гиперплоскость p = {x/ < c, x> = < c, х0> }. Множество Y=XÇ p является ограниченным, замкнутым, выпуклым множеством, как пересечение ограниченного замкнутого выпуклого множества Х а выпуклым, замкнутым множеством p. Кроме того YÌ Еn-1 определяется гиперплоскостью p, поэтому в Y найдутся угловые точки хi такие, что х0= Покажем, что xi (i= xi= (1-a) x' + a х'', x', x'' Î X, aÎ (0, 1) (3.22) По крайней мере одна из этих точек не принадлежит p, в противном случае xi не угловая для Y. Пусть x' Ï p тогда, так как p - опорная гиперплоскость к Х, а x'Î X, то < c, x'> < < c, x0> (3.23) Вычислим значение < c, xi>: < c, xi> = < c, (1-a) x'+ a х'' > = (1-a)< c, x' > + a< c, x''> (3.24) Откуда следует < c, xi> < < c, x0>, (3.25) то есть xi Ï p, что противоречит тому, что xi Î Y=XÇ p. Этим мы доказали, что угловые точки множества Y являются и угловыми точками множества Х. Таким образом, для граничной точки теорема верна. 2. Пусть x0Î X 0. Проведем через x0 произвольную прямую l. Так как Х – ограниченное множество, то найдутся точки х' и х'', являющиеся пересечением границы Х с l. Тогда найдется g Î (0, 1) такая, что x0= (1-g) x'+ g х'' (3.26) Для граничных точек х' и х'' теорема верна, поэтому x’= где xi (i= aI ³ 0, (i= Заметим, что среди точек xi, yj могут быть совпадающие, отсюда получим x0= (1-g) x' + g х'' = Здесь ai./ (1-g)-1³ 0, i= Выполнив несложные преобразования, получим
Таким образом, получаем, что x0 является выпуклой комбинацией конечного числа угловых точек xi (i=
|

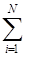 ai xi, aI ³ 0, (i=
ai xi, aI ³ 0, (i=  ),
),  bj yj (3.27)
bj yj (3.27) ), yj (j =
), yj (j = 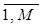 ) – угловые точки множества X.
) – угловые точки множества X. ),
),  bj=1. (3.28)
bj=1. (3.28) bj /g--1 =1 (3.30)
bj /g--1 =1 (3.30)


