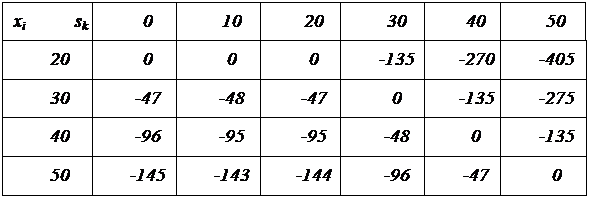Критерий Лапласа

max { u (x_i, S_k)/ x_i} (2.25)

Критерий Сэвиджа:

max {min {u_c (x_i, S_k)/, S_k}/ x_i}, (2.26)

x_i S_k

где u_c (x_i,, S_k) = u (x_i, S_k) - max u (x_i, S_k), i=1, 2,...

Рассмотрим использование данных критериев в условиях неопределенности для практической ситуации.

Пример 2.2. Некоторая фирма решает построить отель в одном из курортных мест. Необходимо определить наиболее целесообразное количество мест или комнат в этой гостинице.

Составляют смету расходов по строительству гостиницы с различным количеством комнат, а также рассчитывают ожидаемый доход в зависимости от количества комнат, которые будут сняты.

В зависимости от принятого решения — количества комнат в гостинице x=20, 30, 40, 50 и количества снятых комнат S=0, 10, 20, 30, 40, 50, которое зависит от множества случайных факторов и неизвестно фирме, получают таблицу 2.5. ежегодных прибылей:

Таблица 2.5

x s	0	10	20	30	40	50
20	-121	62	245	245	245	245
30	-168	14	198	380	380	380
40	-216	-33	150	332	515	515
50	-264	-81	101	284	468	650

 

Определим наиболее подходящее количество комнат в гостинице по выше приведенным критериям.

Критерий Вальда.

max min l_ik = -121, Xопт=20.

x_i s_k

Судя по результатам, критерий Вальда не применим, так как в этом случае от постройки гостиницы следует отказаться.

Критерий Лапаласа.

max l_ik = max l_k =max(153, 198, 210, 193) = 210, Xопт =40.

x_i x_i

Критерий Гурвица.

max [a max l_ik + (1 — a) min l_ik],

x_i k k

Тогда для разных a можно построить таблицу доходов по критерию Гурвица

H= ||h_ia||,

где h_ia = [a max l_ik + (1 — a) min l_ik

k k

Таким образом для различных значений a получим таблицу 2.6.

Таблица 2.6.

x s	0, 1	0, 2	0, 5	0, 9
20	-84	-47	62	206
30	-114	-59	108	325
40	-143	-70	150	442
50	-172	-81	193	560

Вычислим по формуле 2.24 оптимальное количество комнат в гостинице в зависимости от a. Результаты представлены в таблице 2.7. Таблица 2.7.

a	0, 1	0, 2	0, 5	0, 9
Х опт	20	20	50	50

Таким образом, при a = 0, 1 получено консервативное решение, равное по значению к критерию Вальда Х опт =20. Соответственно при a =0, 9 полученооптимистичное решение.

При a =1 критерий Гурвица становится слишком оптимистичным, так как рассчитывает на наилучшие из наилучших условий.

При отсутствии ярко выраженной склонности к оптимизму или пессимизму рекомендуется выбирать. Для нашего примера в этом случае оптимальное решение Xопт =50.

 

Критерий Сэвиджа. Строим матрицу сожалений (таблица 2.8.):

Таблица 2.8.

 

max min u_{i k c} = max {-405, -275, -135, -145} = -135.

^{X i Sk}

Таким образом, предстоит сделать выбор между различными решениями:

по критерию Вальда строить 20 комнат;

по критерию Лапласа строить 40 комнат;

по критерию Гурвица строить 20 комнат, если заказчик - пессимист и 50 комнат, если заказчик оптимист;

по критерию Сэвиджа 40 комнат.

Какое из возможных решений предпочтительнее? Это определяется выбором соответствующего критерия (Вальда, Лапласа, Гурвица или Сэвиджа).

Варианты заданий для лабораторной работы