Методика определения полезностиДля принятия решений необходимо установить предпочтительность различных критериев (меру полезности тех или иных исходов) для лица, принимающего решение. Методика определения полезности разработана в работе [18]. Практическое применение теории полезности основывается на следующих аксиомах [27]: 1) Результат xi оказывается предпочтительнее xj тогда и только тогда, когда u(xi) ³ u(xj), где u(xi) и u(xj) – полезности результатов xi и xj соответственно. 2) Транзитивность: если xi> xj , а xj > xk , то u(xi) > u(xk). 3) Линейность: если некоторый результат х представлен в виде x=(1-k)x1+ kx2, где 0 £ k £ 1, то u(x1) = (1-k) u(x1)+ k u(x2). 4) Аддитивность: если u(x1, u2) – полезность от достижения одновременно результатов x1 и x2 , то свойство аддитивности следующее: u(x1, x2) = u(x1)+ u(x2). (2.12) Аналогично, если имеется n результатов, x1, x2, …, xn, достигаемых одновременно, то u(x1, x2, …, xn) = u(x1 + x2 + … + xn)= Рассмотрим несколько вариантов алгоритмов определения полезности для различных случаев.
I. Случай, когда имеются два результата. Тогда алгоритм определения полезности имеет вид: Шаг 1. Определим, какой результат предпочтительнее для лица, принимающего решение. Пусть x1 > x2, т. е. x1 предпочтительнее, чем x2. Шаг 2. Определим такую вероятность a, при которой достижение результата x1 будет эквивалентно достижению результата x2, получаемому с вероятностью 1. Шаг 3. Оценим соотношение между полезностями результатов x1 и x2. Для этого примем полезность u(x2 )=1. Тогда au(x1 )= u(x2 ), откуда u(x1 )= II. Случай, когда имеется n возможных результатов x1, x2, …, xn, между которыми установлено отношение предпочтения x1> x2> … > xn. Тогда алгоритм определения полезности заключается в следующем: Шаг 1. Определяем величину a1 из условия a1 u(x1 ) = u(x2 ) Шаг 2. Аналогично определяем a2 из условия a2 u(x2 ) = u(x3 ), ........................, an-1 из условия an-1 u(xn-1)= u(xn ). Шаг 3. Положив полезность наименее предпочтительного результата xn равной единице, находим u(xn )=1, u(xn-1 )= III. Случай, когда некоторые критерии являются качественными. Применяется методика, основанная на алгоритме, предложенном Р. Акофом и Р. Черчменом [18]. Таблица 2.1.
Пусть имеется n результатов x1 , x2 , …, xn. Алгоритм определения полезности заключается в следующем: Шаг 1. Упорядочивают все результаты по убыванию предпочтительности. Пусть x1 - наиболее, а xn – наиболее предпочтительный результат.Составляют таблицу возможных комбинаций результатов, достигаемых одновременно, и затем устанавливают их предпочтение относительно отдельных результатов x1, x2, …, xn (см. таблицу 2.1.). Информацию о предпочтительности результатов предоставляют эксперты. Шаг 2. Приписывают начальные оценки полезности отдельных результатов u0(x1), u0(x2), …, u0(xn). Затем подставляют начальные оценки в последнее соотношение таблицы 2.1. Если это соотношение удовлетворяется, то оценки остаются без изменения. В противном случае производят коррекцию полезностей таким образом, чтобы удовлетворялось данное соотношение. Шаг 3. Переходят к следующему соотношению. Процесс коррекции продолжается до тех пор, пока не образуется оптимальная система оценок u*(x1), u*(x2), …, u*(xn). Пример 2.1. Пусть эксперт упорядочивает пять результатов x1 , x2 , x3, x4, x5, приписав им следующие оценки: u0(x1)=7; u0(x2)=4; u0(x3)=2; u0(x4)=1, 5; u0(x5)=1. Рассмотрев возможные варианты выбора, он высказал следующее суждение относительно ценности тех или иных комбинаций результатов: 1) x1 < x2 + x3 + x4+ x5, 2) x1 < x2 + x3 + x4, 3) x1 < x2+x3 + x5, 4) x1 > x2 + x3, 5) x2 < x3 + x4+ x5, 6) x2 > x3 + x4, 7) x3 > x4+ x5. Нужно произвести оценку полезности результатов так, чтобы удовлетворить всем неравенствам. Подставим начальные оценки в неравенство 7): u0(x3)=2 < u0(x4) + u0(x5)=1, 5+1=2, 5. Следовательно неравенство 7) не удовлетворяется. Изменим полезность результата x3: u0(x3)=3 и проверим неравенство 6): u0(x2)=4 < u1(x3) + u0(x4)=3+1, 5=4, 5 Неравенство 6) также не удовлетворяется, поэтому выполним коррекцию u1(x2)=5, при этом неравенство 5) тоже удовлетворяется. Рассмотрим неравенство 4): u0(x1)=7< u1(x2) + u1(x3)=5+3=8. Оно не выполняется, поэтому примем u1(x1 )= 8, 5. Теперь неравенства 3), 2), 1) тоже удовлетворяются. Проверим ещё раз неравенства 6) и 7) при измененных значениях полезностей: 5> 3+1, 5 и 3 > 1, 5 + 1. Оба неравенства выполняются. Выпишем окончательные оценки полезности результатов: u1(x1)=8, 5; u1(x2)=5; u1(x3)=3; u1(x4)=1, 5; u1(x5)=1. Рассмотренная методика определения полезности применима, когда количество результатов n ограничено n £ 7. В случаях, когда количество результатов n > 7 в работе [18] предложена модификация рассмотренного алгоритма, которая заключается в следующем. 1. Множество результатов разбивают на подмножества, состоящие из 5 - 7 результатов и имеющие один общий результат, например, x1. 2. Затем приписывают начальные значения полезности для всех результатов, причем полезность общего результата x1 одинакова во всех подмножествах. 3. Далее применяют способ коррекции оценок полезности независимо в каждом подмножестве с ограничением u(x1 )=const. 4. В результате получают систему полезностей с единой мерой для всех подмножеств u(x1 ).
|
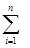u(xi). (2.13)
.
,..., u(x1 )= 
. (2.14)
