Принятие решений в условиях неопределенности
Выбор критерия принятия решений является наиболее сложным и ответственным этапом в исследовании операций. При этом не существует каких-то общих рекомендаций или советов. Выбор критерия должен производить заказчик на самом высоком уровне и в максимальной степени согласовывать этот выбор с конкретной спецификой задачи, а также со своими целями. В частности, если даже минимальный риск недопустим, то следует применять критерий Вальда. Если наоборот, определенный риск вполне приемлем и заказчик намерен вложить в некоторое предприятие столько средств, чтобы потом он не сожалел, что вложено слишком мало, то выбирают критерий Сэвиджа. При отсутствии достаточной информации для выбора того или иного критерия возможен альтернативный подход, который связан с вычислением шансов на успех и разорение на основе прошлого опыта. Существует несколько критериев для выбора оптимальной стратегии. Как было сказано выше, отличаются они по степени консерватизма. Рассмотрим более подробное описание названных критериев. Критерий Вальда (критерий осторожного наблюдателя). Этот критерий оптимизирует полезность в предположении, что среда находится в самом невыгодном для наблюдателя состоянии. По данному критерию решающее правило имеет следующий вид: max{min { u (xi, Sk)/Sk}/ xiÎ X}, (2.18) xi sk гдеu (xi, Sk) = По критерию Вальда выбирают стратегию, которая дает гарантированный выигрыш при наихудшем варианте состояния среды. Критерий Гурвица основан на следующих двух предположениях: среда может находиться в самом невыгодном состоянии с вероятностью (1 - a) и самом выгодном — с вероятностью a, где a коэффициент доверия. Тогда решающее правило записывается так: max {[a max {u (xi, Sk)/Sk} + (1 — a) min {u(xi, Sk)/Sk}]/xi}, (2.19) xi Sk Sk где 0 ≤ a ≤ 1. Если a = 0, получаем критерий Вальда. Если a = 1, то приходим к решающему правилу вида: max {max {u (xi, Sk)/xi}/Sk}, (2.20) xi Sk так называемая стратегия «здорового оптимиста», который верит в удачу. Критерий Лапласа. Если неизвестны состояния среды, то все состояния среды считают равновероятными: p(Si) = p(Sj) =…= p(Sk). В результате решающее правило определяется соотношением max{ xi xi при условии р (Sk) = Критерий Сэвиджа (критерий минимизации «сожалений»). «Сожаление» - это величина, равная изменению полезности результата при данном состоянии среды относительно наилучшего возможного состояния. Чтобы определить «сожаление», поступают следующим образом: 1. Строим матрицу 2. В каждом столбце этой матрицы найдем максимальный элемент uk = max {ui k /i= i 3. Далее строим матрицу «сожалений» uc = ||uikc||, uikc= uik - uk. 4. Искомую стратегию xi, которая минимизирует «сожаление», определим из условия min {max {u ik / xi}/Sk } sk xi Этот критерий минимизирует возможные потери при условии, что состояние среды наихудшим образом отличается от предполагаемого. Рассмотрим частный случай предложенной выше модели задачи в условиях неопределенности. Предположим, что каждому возможному состоянию среды соответствует один возможный исход: Р (0j/Sk) = d jk,, (2.21) где Таким образом, в данном случае математическая модель задачи принятия решений определяется множеством стратегий X = {xi}, множеством состояний среды S = {Sk}, а также следующей матрицей (таблица 2.4):
Таблица 2.4.
L =
где lij= и(xi, Sj). Множество {р (Sj)} предполагается неизвестным. В этом случае критерии для выбора оптимальной стратегии имеют следующий вид: Критерий Вальда max {min u (xi, Sk)/ Sk }/ xi} (2.23) xi Sk Критерий Гурвица имеет вид max {[a max {u(xi, Sk)/Sk} + (1 — a) min {u(xi, Sk)/Sk}]/xi}, (2.24) xi Sk Sk
|

 и (Оj , xi) p (j /xi, Sk).
и (Оj , xi) p (j /xi, Sk). u(Oj, xi) р (0j, /xi, Sk) p(Sk)/ xiÎ X}=max E{u(xi)/ xiÎ X}. (2.21)
u(Oj, xi) р (0j, /xi, Sk) p(Sk)/ xiÎ X}=max E{u(xi)/ xiÎ X}. (2.21) .
. =|| uik ||, где uik = и(xi, Sk) i =
=|| uik ||, где uik = и(xi, Sk) i =  ; k =
; k =  ;
;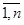 } и вычтем его из всех элементов этого столбца.
} и вычтем его из всех элементов этого столбца.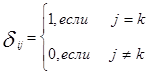 (2.22)
(2.22)



