Выпуклые множества
Рассмотрим множество вида [x, y]={z/z=(1-a)x+ay, aÎ [0, 1], zÎ En}. (3.1)
z(a)=x+a(y-х)=(1-a)x+ay, (3.2) причемпри a =0 Z(a)=x, при a=1 Z(a)=у. Если a пробегает значения между 0 и 1, то Z(a) пробегает значения по прямой между x и y.
Если при этом (х, y)Ì X0 (X0- множество z(a) внутренних точек множества Х), то Х называется строго выпуклым множеством.
Рис. 3.1. при aÎ (0, 1) z(a) является внутренней точкой множества Х. На рис. 3.2. приведен пример выпуклого множества, а на рис. 3.3 пример множества, не являющегося выпуклым.
Рис. 3.2 Рис. 3.3. Для выпуклых множеств справедливы следующие теоремы: Теорема 3.1. Пересечение любого числа выпуклых множеств выпукло. Доказательство. Пусть Z = Ç Хl Возьмем х, уÎ Z и aÎ [0, 1]. lÎ L Покажем, что z(a)= (1-a)x + a y. Действительно, т. к. х, уÎ Z, то для любого lÎ L х, уÎ Хl. Из выпуклостимножеств Хl следует, что z(a)Î Хl для всех lÎ L, поэтому z(a)Î Z, откуда следует выпуклость множества Z. Теорема 3.2. Множество Х={x / < a, x> £ b, xÎ En }, где а – заданный вектор, b - скаляр, является выпуклым множеством. Доказательство. Пусть х, уÎ Z и aÎ [0, 1], докажем, что z(a)= (1-a)x + ay. Действительно < z(a), a> = < (1-a)x + a y, a> = (1-a)< x, a> + a < y, a> Так как х, уÎ Х, то есть < x, a> £ b, < у, a> £ b, то < z(a), a> £ b, т.е. z(a)Î Х. Следствие 3.1. Множество Х={x / Ах £ b, xÎ En }, где А – матрица размерности m× n, bÎ En выпукло. Определение 3.2. Точка z = Теорема 3.3. Выпуклое множество содержит любые выпуклые комбинации любых своих точек. Доказательство. Пусть Х – выпуклое множество, содержащее элементы хi,, i= a2 = a, a1 = 1- a. Пусть утверждение верно для некоторого n ³ 2, покажем его справедливость для n+1. Пусть Z= Z= По предположению точка x' =
В силу выпуклости Х и определения 3.1 следует, что ZÎ X. Теорема 3.4. Замыкание
z(a)= (1-a)x + a y Î
|

 Это отрезок прямой, проходящей через точки x и y, так как уравнение прямой, проходящей через точки x и y имеет вид:
Это отрезок прямой, проходящей через точки x и y, так как уравнение прямой, проходящей через точки x и y имеет вид: Определение 3.1. Множество ХÎ Еn называется выпуклым, если для любых
Определение 3.1. Множество ХÎ Еn называется выпуклым, если для любых х точек х, уÎ Х отрезок [х, y ]Î Х.
х точек х, уÎ Х отрезок [х, y ]Î Х. y Из этого определения следует, что у выпуклого множества для любых х, уÎ Х и aÎ [0, 1] точка z(a) = (1-a)x + a y Î Х, если Х – строго выпуклое множество, то
y Из этого определения следует, что у выпуклого множества для любых х, уÎ Х и aÎ [0, 1] точка z(a) = (1-a)x + a y Î Х, если Х – строго выпуклое множество, то

 ai xi называется выпуклой комбинацией точек х1, х2, …, хn Î En, если ai ³ 0, i =
ai xi называется выпуклой комбинацией точек х1, х2, …, хn Î En, если ai ³ 0, i =  ,
,  ai = 1.
ai = 1.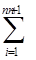 ai xi, где xi Î X, ai ³ 0, i=
ai xi, где xi Î X, ai ³ 0, i=  ai=1,
ai=1, xi + an+1 xn+1.
xi + an+1 xn+1.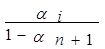 ³ 0, i =
³ 0, i = 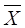 выпуклого множества Х выпукло.
выпуклого множества Х выпукло.


 Доказательство. Пусть х, у Î
Доказательство. Пусть х, у Î 


