Смешанных стратегий
Не все матричные игры имеют ситуацию равновесия в чистых стратегиях. Всякая матричная игра имеет ситуацию равновесия в смешанных стратегиях. Задача линейного программирования эквивалентна в определенном смысле матричной игре. Действительно, рассмотрим следующие прямую и двойственную задачи линейного программирования
min xu max yw
xA≥ w, Ay≤ u,
x≥ 0; y≥ 0
Рассмотрим матричную игру, определенную матрицей А> 0.
A= 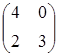
Соответствующие ей задачи линейного программирования имеют следующий вид:
min x1+ x2 max y1+ y2
  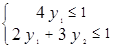
x1, x2≥ 0, y1, y2≥ 0.
Решением этой задачи является:
x1 =1/12, x2 =1/3;
y1 =1/4, y2 =1/6; Значение функционала Q=5/12.
Оптимальные стратегии игроков тогда определяются так:
X*=X/Q, Y*=Y/Q.
x1* =1/5, x2* =4/5, y1* =3/5, y2* =2/5.
Если А ≤ 0, т.е. есть существуют aij≤ 0, то строим А'=A+B, где А'={ a'ij}, a'ij> 0.
Задание 6
Найти решение матричной игры в смешанных стратегиях для следующих матриц:
1.A=  , ,
| 2.A=  , ,
| 3.A= 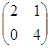 , ,
| 4.A= 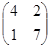 , ,
| 5.A= 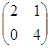 , ,
| 6.A=  , ,
| 7.A=  , ,
| 8.A=  , ,
| 9.A= 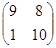 , ,
| 10.A=  , ,
| 11.A= 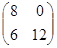 , ,
| 12.A=  , ,
| 13.A= 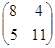 , ,
| 14.A=  , ,
| 15.A= 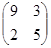 , ,
| 16.A=  , ,
| 17.A=  , ,
| 18.A=  , ,
| 19.A=  , ,
| 20.A=  , ,
| 21.A=  , ,
| 22.A=  , ,
| 23.A=  , ,
| 24.A=  , ,
| 25.A=  . .
|
|
|
|
1.A=  , ,
| 2.A=  , ,
| 3.A=  , ,
| 4.A=  , ,
| 5.A=  , ,
| 6.A=  , ,
| 7.A=  , ,
| 8.A= 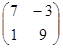 , ,
| 9.A=  , ,
| 10.A=  , ,
| 11.A=  , ,
| 12.A=  , ,
| 13.A=  , ,
| 14.A=  , ,
| 15.A=  , ,
| 16.A=  , ,
| 17.A=  , ,
| 18.A=  , ,
| 19.A=  , ,
| 20.A=  , ,
| 21.A=  , ,
| 22.A=  , ,
| 23.A=  , ,
| 24.A=  , ,
| 25.A=  . .
|
|
|
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|
Ситуация 26. ПРОВЕРЕНО МИНЗДРАВОМ
Станислав Свердлов закончил российско-американский факультет менеджмента Томского государственного университета...
Различия в философии античности, средневековья и Возрождения ♦Венцом античной философии было: Единое Благо, Мировой Ум, Мировая Душа, Космос...
Характерные черты немецкой классической философии 1. Особое понимание роли философии в истории человечества, в развитии мировой культуры. Классические немецкие философы полагали, что философия призвана быть критической совестью культуры, «душой» культуры.
2. Исследовались не только человеческая...
|
Типовые примеры и методы их решения. Пример 2.5.1. На вклад начисляются сложные проценты: а) ежегодно; б) ежеквартально; в) ежемесячно Пример 2.5.1. На вклад начисляются сложные проценты: а) ежегодно; б) ежеквартально; в) ежемесячно. Какова должна быть годовая номинальная процентная ставка...
Выработка навыка зеркального письма (динамический стереотип) Цель работы: Проследить особенности образования любого навыка (динамического стереотипа) на примере выработки навыка зеркального письма...
Словарная работа в детском саду Словарная работа в детском саду — это планомерное расширение активного словаря детей за счет незнакомых или трудных слов, которое идет одновременно с ознакомлением с окружающей действительностью, воспитанием правильного отношения к окружающему...
|
|

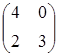


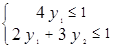
 ,
,
 ,
,
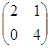 ,
,
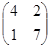 ,
,
 ,
,
 ,
,
 ,
,
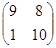 ,
,
 ,
,
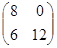 ,
,
 ,
,
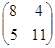 ,
,
 ,
,
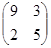 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
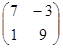 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.



