Матрицы. Действия над матрицами. Решение матричных уравнений
1) Над матрицами
2) Какими характеристиками должны обладать матрицы, чтобы их можно было перемножить? Сформулируйте правило умножения матриц. Выполните умножение матриц:
Ответы: 3) Какими свойствами обладает операция умножения матриц: коммутативность, ассоциативность, дистрибутивнось? Применяя нужные свойства, выполните умножение матриц:
4) Выполнить операцию возведения в степень
Занятие 16. Обратная матрица. Системы линейных уравнений: метод обратной матрицы, метод Крамера 1) Дайте определение обратной матрицы
Ответы:
2. Системы линейных уравнений
Каждую систему линейных уравнений решите тремя способами: · Методом обратной матрицы · Методом Крамера
, Занятие 17. Системы линейных уравнений: метод Гаусса, ранг матрицы, теорема Кронекера-Капелли
1. Каждую систему линейных уравнений решите методом Гаусса:
2. Дайте определение понятия ранг матрицы. Найдите ранг матрицы методом элементарных преобразований: а)
3. Для каждой из указанных ниже систем · методом элементарных преобразований определите ранг матрицы системы и ранг расширенной матрицы, · на основании теоремы Кронекера-Капелли сделайте вывод о совместности системы (определите число решений системы), · найдите решения системы, при этом, если решений множество, то укажите число базисных и свободных переменных
,
Ответы: не имеет решений, множество решений,
Занятие 18. Векторы: линейные операции
1. По заданной паре векторов
2. При каких значениях параметров
3. Даны смежные вершины параллелограмма 4. По координатам середин сторон треугольника Ответ: 5. Координаты вершин треугольника
6. В трапеции
7. Найти координаты вектора
8. Найти координаты вектора
Занятия 19. Скалярное произведение векторов 9. При каких значениях
10. Найти угол при вершине
11. Векторы
12. Найдите длины диагоналей параллелограмма, построенного на векторах Ответ: 13. Найдите проекцию
Занятия 20. Векторное и смешанное произведения векторов 14. Найдите площадь параллелограмма, диагоналями которого служат векторы
15. Найти
16. Координаты вершин треугольника
17. В точке 18. Определить, лежат ли точки
19. Найдите объем тетраэдра с вершинами
20. При каких значениях параметра 21. Координаты вершин тетраэдра Занятие 21. Прямая и плоскость в пространстве 1. Указать особенности в расположении плоскостей и схематично их построить:
а) 3Х–Z=0; б) 2Х=0; с) 2Х–6=0; д) Х–2У=0; е) Х–2У–2=0;
ж) 2Х+Z–2=0; з) 2Х+3У+2Z–6=0;
2. Составьте уравнение плоскости, проходящей через:
а) М(1; -1; 2) параллельно плоскости ОХУ; б) М(4; -1; 2) и ось ОХ; в) М1(7; 2; -3); М2(5; 6; -4) параллельно ОХ; г) М1(1; -1; 2); М2(3; 0; -3) параллельно д) М1(1; -3; 2); М2(5; 1; -4); С(2; 0; 3) Найдите расстояние от М0(1; 0; -2) до найденной плоскости е) М0(-2; 7; 3) параллельно плоскости Х–4У+5Z–1=0 ж) М0(3; 4; 0) перпендикулярно плоскостям Х+У+5Z–9=0; 2Х+У+2Z+1=0 3. Найти углы, образованные нормалью а)
4. Покажите, что плоскости параллельны и найдите расстояние между ними: 2Х–3У+6Z–14=0 4Х–6У+12Z+21=0;
5. Найдите угол между плоскостями: Х–3У+6Z–14=0 2Х–У+Z=0.
6. Напишите уравнение прямой, проходящей: а) М1(2; 1; 3); М2(3; 0; 1); б) М0(3; 1; 0) ç ç в) М0(3; 1; 0) ^ плоскости 4Х+3У–Z=0;
7. Найдите точку М¢ (Х; У; Z), симметричную М(1; 5; 2) относительно плоскости 2Х–У–Z+11=0
8. Запишите канонические и параметрические уравнения прямой:
Занятие 22. Прямая линия на плоскости 1. Написать уравнения прямой линии на плоскости: в) проходящей через произвольную точку г) пересекающей координатные оси в точках
д) проходящей через начало координат и точку пересечения прямых
2. В треугольнике с вершинами
3. По координатам смежных вершин
4. Найдите точку, симметричную точке
5.Перепишите уравнение прямой линии
6.Покажите, что прямые линии
Занятие 23. Кривые второго порядка
1. Уравнение 2. Постройте кривые и укажите их основные характеристики
3. Установите, какие линии определяются уравнениями и схематично постройте эти линии: ü ü ü ü ü 4. Составьте уравнение окружности, которая имеет центр на прямой Ответ:
Занятие 24. Контрольная работа «Векторная алгебра и аналитическая геометрия». Работа состоит из 5 задач: 1.Действия над матрицами (умножение, обратная матрица), решение систем алгебраических уравнений (методы Крамера, Гаусса, матричный метод) 2. Длина вектора. Координаты вектора. Линейные операции над векторами. Скалярное произведение. 3.Векторное и смешанное произведения векторов 4. Прямая линия на плоскости. Кривые второго порядка 5.Прямая линия и плоскость в пространстве Занятие 25. Частные производные первого порядка. Градиент. Производная по направлению. 1. Найдите и схематично постройте область определения функции, дайте её характеристику (связность, замкнутость, ограниченность): а) г)
2. Найдите уравнение линии уровня (или поверхности уровня) для указанных функций, проходящих через заданные точки. Постройте линию уровня на чертеже вместе с областью определения: а) г) 3. Для указанных функций найти частные производные первого порядка; Записать полный дифференциал первого порядка. а) в) е) и)
4. Найдите производную указанной функции по данному направлению в точке М0: а) б)
5. Найдите градиент функции в указанной точке:
а) б) в)
6. Найти нормаль к поверхности и написать уравнение касательной плоскости для указанной функции, в указанной точке:
а) б)
Занятие 26. Локальные экстремумы функции двух переменных 1. Исследуйте функцию на локальный экстремум:
2. Исследуйте функцию на условный экстремум:
Z=6–5X–4У; j(Х, У)=Х2-У2–9=0; L=6–5Х–4У+l(Х2-У2–9)
3. Найдите наименьшее m и наибольшее М значения функции в замкнутой ограниченной области:
Ответы: Задача 1: а) (-2; 0) – минимум; б) (4; 4); (-4; -4) – минимумы; в) г) (1; -1; 3) – минимум.
Задача 2.( 5; -4); (-5; 4);
Задача 3. M=6; m=-1;
|

 и
и  выполнить действия
выполнить действия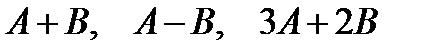
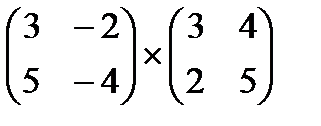 ,
, 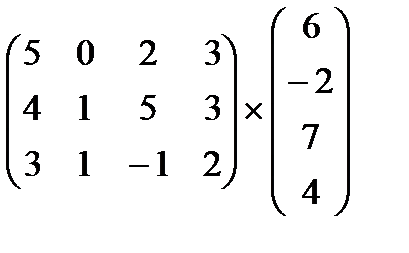 ,
, 
 ,
, 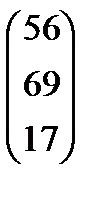 ,
, 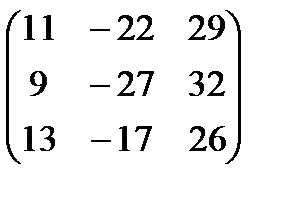
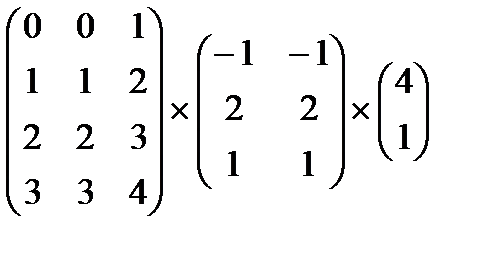 Ответ:
Ответ: 
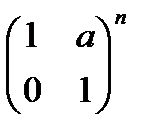 Ответ:
Ответ: 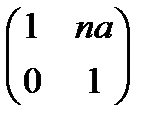

 и условия ее существования. Для указанных матриц проверьте выполнение условий существования обратной матрицы и, если обратная матрица существует, то найдите:
и условия ее существования. Для указанных матриц проверьте выполнение условий существования обратной матрицы и, если обратная матрица существует, то найдите: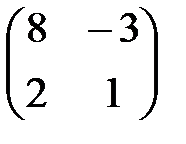 ,
, 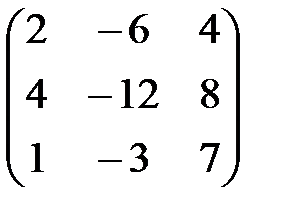 ,
, 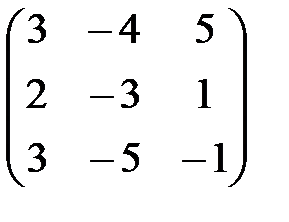
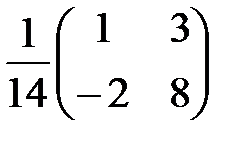 ,
, 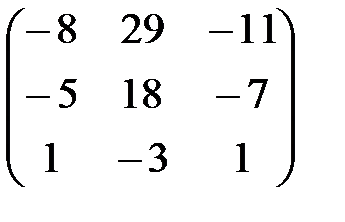

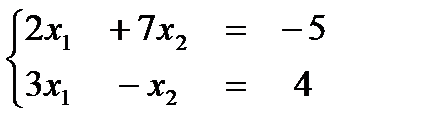
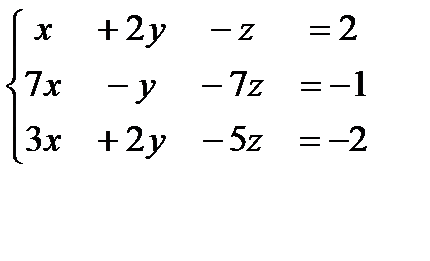
 , б)
, б)  , в)
, в)  , д)
, д) 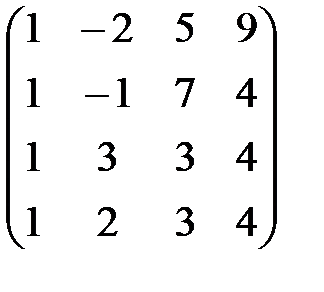
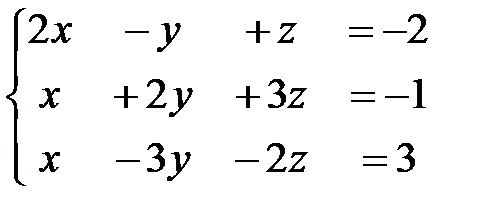 ,
, 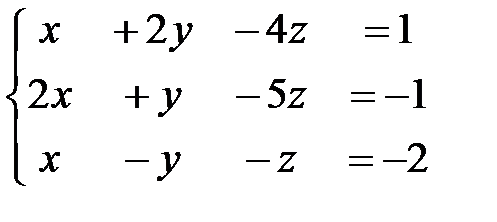

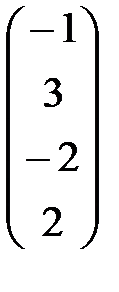 .
. ,
,  найти декартовы координаты векторов
найти декартовы координаты векторов 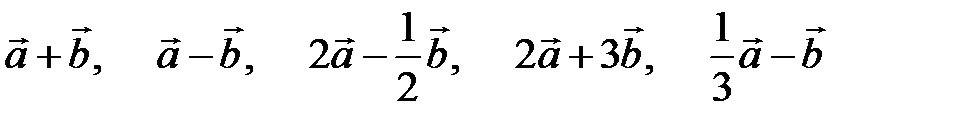 , их длину и соответствующие единичные векторы (орты), укажите направляющие косинусы.
, их длину и соответствующие единичные векторы (орты), укажите направляющие косинусы.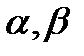 векторы
векторы  ,
, 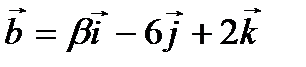 коллинеарны?
коллинеарны?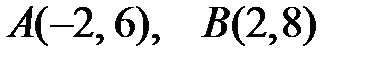 и точка пересечения его диагоналей
и точка пересечения его диагоналей  . Найдите координаты двух других вершин и длины сторон. Ответ:
. Найдите координаты двух других вершин и длины сторон. Ответ: 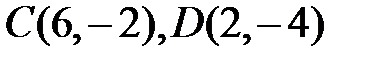
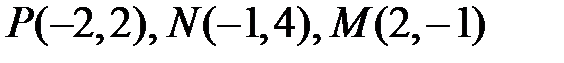 найдите координаты его вершин и длины сторон.
найдите координаты его вершин и длины сторон.
 ,
, 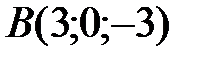 ,
,  . Найти длину медианы, проведенной из вершины
. Найти длину медианы, проведенной из вершины 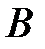 .
.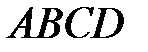 отношение длин оснований
отношение длин оснований 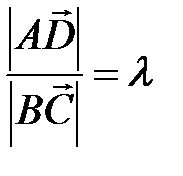 , векторы диагоналей
, векторы диагоналей  ,
, 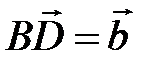 . Выразить через векторы
. Выразить через векторы  векторы сторон трапеции. Ответ:
векторы сторон трапеции. Ответ: 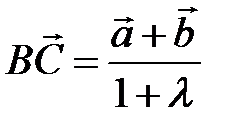 и т.д.
и т.д.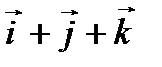 относительно косоугольного базиса
относительно косоугольного базиса 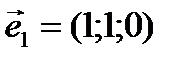 ,
, 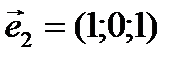 ,
, 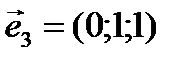 . Чему равны углы между векторами базиса?
. Чему равны углы между векторами базиса? относительно косоугольного базиса
относительно косоугольного базиса  ,
, 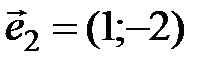 . Ответ:
. Ответ: 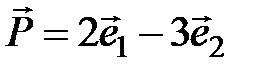
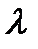 векторы
векторы 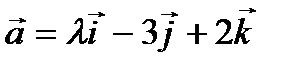 и
и  ортогональны?
ортогональны? в треугольнике с вершинами
в треугольнике с вершинами 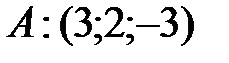 ,
, 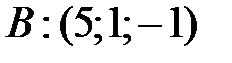 ,
,  . Ответ:
. Ответ: 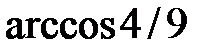
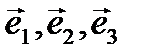 образуют ортонормированный базис. Найти
образуют ортонормированный базис. Найти  , если известны
, если известны  и
и  .
. , если
, если 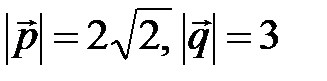 ,
, 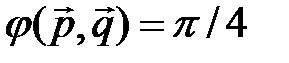 .
.
 , если
, если 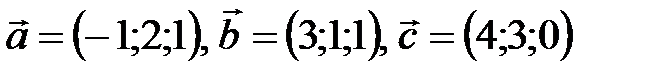 . Ответ:
. Ответ: 
 , где
, где 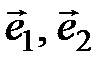 - единичные векторы под углом 45 градусов. Ответ:
- единичные векторы под углом 45 градусов. Ответ: 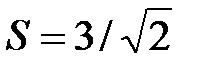
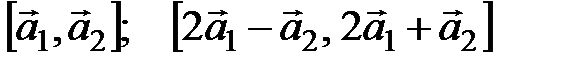 , если
, если  . Ответ:
. Ответ: 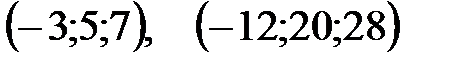
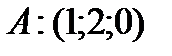 ,
,  ,
, 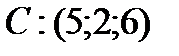 . Найти площадь треугольника и длину его высоты, опущенной из вершины
. Найти площадь треугольника и длину его высоты, опущенной из вершины 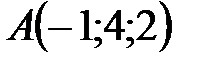 приложена равнодействующая сил
приложена равнодействующая сил 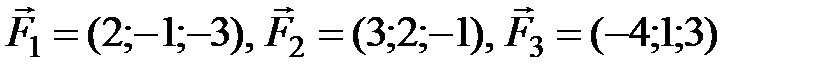 . Найдите вектор момента равнодействующей этих сил относительно точки
. Найдите вектор момента равнодействующей этих сил относительно точки  . Ответ:
. Ответ: 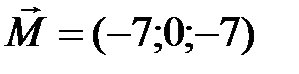
 в одной плоскости?
в одной плоскости? . Ответ:
. Ответ: 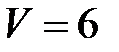
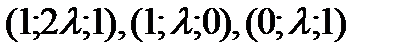 компланарны?
компланарны?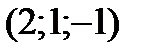 ,
,  ,
, 
 , а его объем равен 5. Найти значение неизвестной координаты.
, а его объем равен 5. Найти значение неизвестной координаты.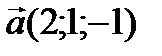 ;
;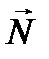 с координатными осями и найти расстояние плоскости от начала координат:
с координатными осями и найти расстояние плоскости от начала координат: ; б)
; б)  ;
;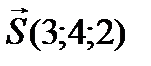 ;
;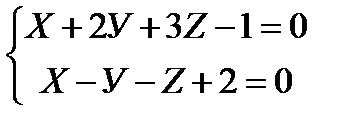
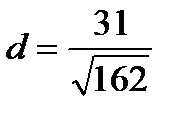 ; ж) 3Х–8У+Z+23=0;
; ж) 3Х–8У+Z+23=0;
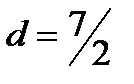 ;
7. M`(-3; 7; 4);
;
7. M`(-3; 7; 4);
 ;
;
 под углом
под углом  к оси ординат;
к оси ординат;  ;
; .
.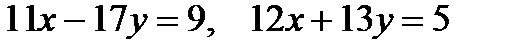 .
. напишите уравнения сторон, высоты
напишите уравнения сторон, высоты 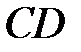 и медианы
и медианы 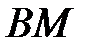
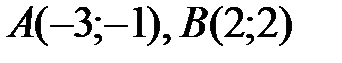 и точки пересечения диагоналей
и точки пересечения диагоналей 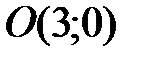 напишите уравнения сторон параллелограмма
напишите уравнения сторон параллелограмма относительно прямой
относительно прямой 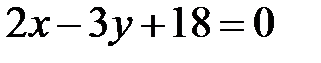 . Ответ:
. Ответ: 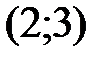
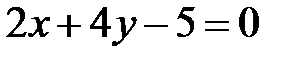 в нормальном виде. Найдите направляющие косинусы нормали к прямой и расстояние от начала координат до прямой.
в нормальном виде. Найдите направляющие косинусы нормали к прямой и расстояние от начала координат до прямой. параллельны и найдите расстояние между ними. Ответ: 3
параллельны и найдите расстояние между ними. Ответ: 3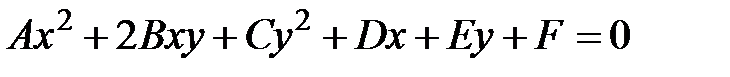 описывает окружность радиуса 5 с центром в точке
описывает окружность радиуса 5 с центром в точке  . Определить все коэффициенты этого уравнения.
. Определить все коэффициенты этого уравнения.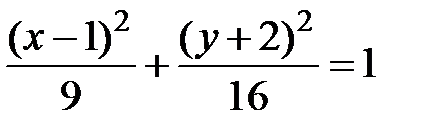 ;
;  ;
; 


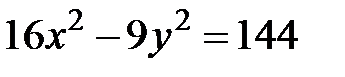
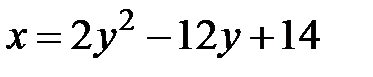
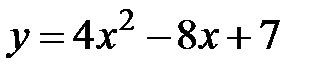
 и касается прямых
и касается прямых 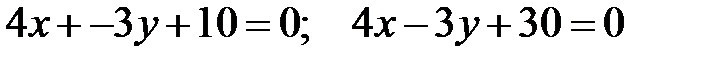 .
.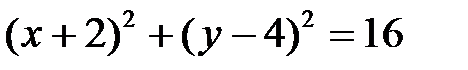
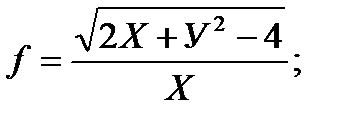 б)
б) 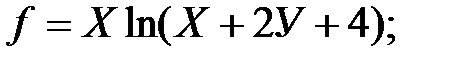 в)
в) 
 д)
д) 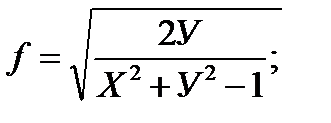
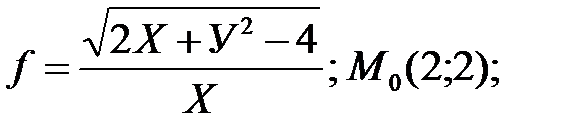 б)
б) 
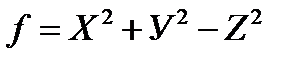 при условии
при условии 
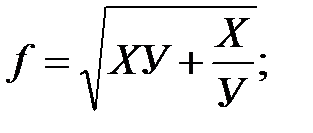 б)
б) 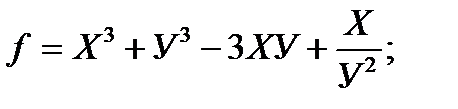
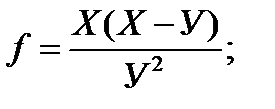 г)
г) 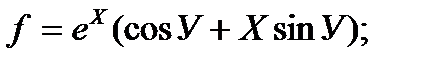 д)
д) 
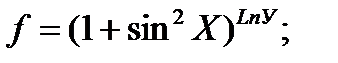 ж)
ж)  з)
з) 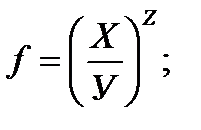
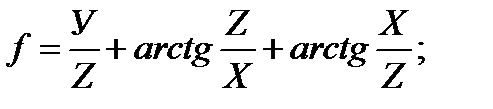 к)
к) 
 если
если 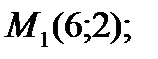
 по направлению
по направлению 
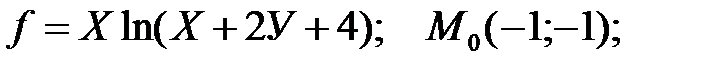
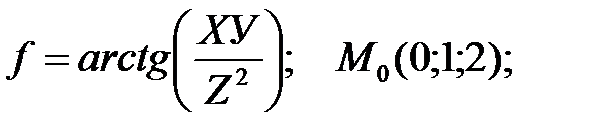

 в точках пересечения с прямой Х=У=2;
в точках пересечения с прямой Х=У=2;
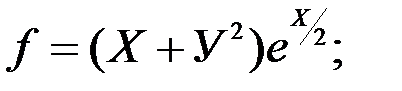 в)
в) 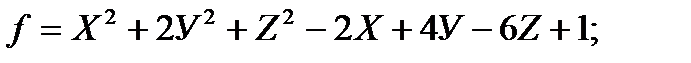
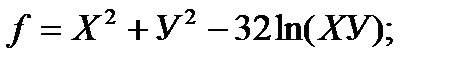
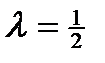 – max
– max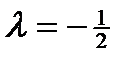 –min
–min

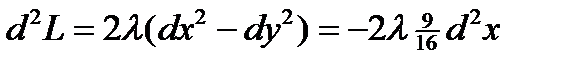 .
.


