Решение. В соответствии с уравнением (10):
В соответствии с уравнением (10): Δ Н откуда Δ Н Подставив значение Δ Н Δ Н Как видно, реакция образования пропана относится к экзотермическим реакциям.
В общем случае тепловой эффект химического процесса зависит от температуры и давления, при которых осуществляется химическое превращение. Влиянием давления на Δ U и Δ Н реакции обычно пренебрегают. Теплоёмкостью с называют количество теплоты, необходимое для нагревания 1г (удельная теплоёмкость) или 1 моля (молярная теплоёмкость) вещества на 1 К. с = С повышением температуры теплоёмкость твёрдых, жидких и газообразных веществ увеличивается. Различают истинную теплоёмкость, т.е. при теплоёмкость при данной температуре с = и среднюю теплоёмкость
которая соответствует конечному интервалу температур. При незначительной величине интервала теплоёмкость считают не зависящей от температуры. В зависимости от условий нагревания теплоёмкость бывает изобарной ср и изохорной сv: ср = сv = Для выведения зависимости теплового эффекта от температуры продифференцируем уравнение (6): Qp = Δ Н = H2 – H1, учитывая уравнение (14), получаем:
Уравнение (17) называют уравнением Кирхгофа, где Δ ср – это разность молярных теплоёмкостей продуктов реакции и исходных веществ с учётом стехиометрических коэффициентов. Для вычисления теплового эффекта при заданной температуре Т, необходимо проинтегрировать уравнение Кирхгофа:
Δ НТ = Δ Н В широком диапазоне температур зависимость теплоёмкости веществ от температуры выражается в виде эмпирических уравнений: ср = a + bT + Коэффициенты a, b, c, c' для продуктов реакции и исходных веществ приводятся в справочниках, далее вычисляют Δ a, Δ b, Δ c, Δ c' как суммы соответствующих величин для продуктов реакции, умноженные на стехиометрические коэффициенты минус соответствующие значения для исходных веществ. Затем зависимость Δ ср = Δ a + Δ bT + подставляются под знак интеграла в уравнение (19) и производится расчёт Δ НТ по правилам интегрирования. При использовании табличных значений средних теплоемкостей
Δ НТ = Δ Н Для процессов, протекающих при постоянном объёме, соответственно, зависимость теплового эффекта от температуры описывается уравнением: Δ UT =
Пример 3. Определить теплоту, поглощённую при нагревании 100 г двуокиси углерода от 15 до 1000º С при постоянном объёме, если с Решение. Объёмная теплоёмкость равна количеству теплоты, которое необходимо для нагревания на 1º С 1м3 газа, приведённого к нормальным условиям. При повышении температуры от Т1 до Т2 количество поглощаемой теплоты можно рассчитать по формуле: Q = После интегрирования выражение примет вид: Q=[a0 (T2 – T1) + a1 При вычислении по данной формуле температуру можно брать в градусах Цельсия. Число молей углекислого газа определяем по формуле ν = и тогда количество поглощённой теплоты в рассматриваемом процессе будет равно Q =
|

 = 3 Δ Н
= 3 Δ Н  + 4 Δ Н
+ 4 Δ Н  – Δ Н
– Δ Н  – 5 Δ Н
– 5 Δ Н  ,
, . (12)
. (12) (13)
(13) (14)
(14) , (15)
, (15) . (16)
. (16)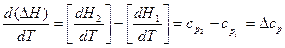 . (17)
. (17)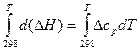 , (18)
, (18)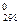
 +
+  . (19)
. (19) c·T2. (20)
c·T2. (20) Δ c·T2 (21)
Δ c·T2 (21) величина Δ
величина Δ 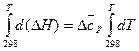 , (22)
, (22) . (23)
. (23) 
 . (24)
. (24)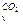 = 27, 24 + 0, 00809t Дж/моль·град.
= 27, 24 + 0, 00809t Дж/моль·град. (для 1 моля вещества)
(для 1 моля вещества)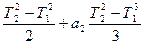 ]
]




