Задача №2. Определение напряжений в грунтовом основании от действия прямоугольной нагрузки приложенной на его поверхности

Определение напряжений в грунтовой толще от действия внешних нагрузок необходимо для установления условий прочности и устойчивости грунтов, определения деформаций и осадок оснований фундаментов.

В большинстве практических случаев при решении вопроса о распределении напряжений в грунтах в механике грунтов применяют теорию линейно деформируемых тел. Для определения напряжений по этой теории будут полностью справедливы уравнения теории упругости, также базирующиеся на линейной зависимости между напряжениями и деформациями (закон Гука).

Определение сжимающих напряжений от действия прямоугольной нагрузки в произвольной точке основания производится на основе метода угловых точек. Значение величин сжимающих напряжений для угловых точек прямоугольной площади загрузки позволяет очень быстро вычислить сжимающие напряжения для любой точки полупространства (грунтового основания) если пользоваться значениями угловых коэффициентов α и α _с.

Для точек расположенных по вертикальной оси под центром загруженного прямоугольника сжимающие напряжения σ _zр = α р

А для точек расположенных по вертикальной оси под углом загруженного прямоугольника

σ _zрс = α _ср

где α – коэффициент, принимаемый по таблице в зависимости от соотношения сторон η = l/b прямоугольной нагрузки (формы подошвы фундамента) и относительной глубины, равной:

ξ =2z/b – при определении σ _zр.

α _с= α /4 – коэффициент, при определении α в данном случае по таблице 2.1 η = l/b, а относительная глубина ξ =z/b.

Характерный вид эпюр σ _zр показан на рисунке 2.1.

Рис. 2.1. Эпюра сжимающих напряжений σ _zр от дествия внешней равномерно-распределенной прямоугольной нагрузки

 

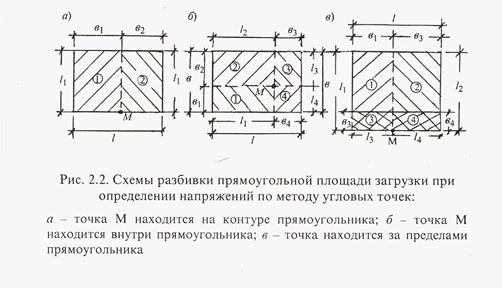
Метод угловых точек для определения сжимающих напряжений σ _zр применяют в случае, когда грузовая площадь может быть разбита на такие прямоугольники, чтобы рассматриваемая точка оказалась угловой. Тогда сжимающее напряжение в этой точке на любой глубине будет равно алгебраической сумме напряжений от прямоугольных площадей загрузки, для которых эта точка является угловой.

Рассмотрим три основных случая:

1) Точка М находится на контуре прямоугольника внешних воздействий (рис. 2.2а);

2) Точка М находится внутри прямоугольника давлений

(рис. 2.2б);

3) Точка М находится вне прямоугольника давлений (рис. 2.2в).

В первом случае величина σ _zр на заданной глубине z под точкой М определяется как сумма двух угловых напряжений, соответсивующих прямоугольника 1 и 2, т.е.:

σ _zрм =(α _с1+α _с2)р

Во втором случае необходимо суммировать угловые напряжения от четырех прямоугольных площадей загрузки 1, 2, 3, 4:

σ _zрм =(α _с1+α _с2+α _с3+α _с4)р

В третьем случае напряжение в точке М складывается из суммы напряжений от действия нагрузки по прямоугольникам 1 и 2, взятых со знаком “плюс”, и напряжений от действия нагрузки по прямоугольникам 3 и 4, взятых со знаком “минус”

σ _zрм =(α _с1+α _с2-α _с3-α _с4)р

Используя исходные данные для конкретного варианта (табл.2.2) определяются напряжения σ _zр под центром и под серединой длинной стороны загруженного прямоугольника в трех точках по глубине основания z=0, 5b; 1, 0b и 2b и строятся эпюры напряжений.

 

Таблица 2.1.