Основные формулы кинематики
Движения тел классифицируют по форме траектории и виду кинематических зависимостей (законов движения). По форме траектории различают прямолинейное и криволинейное движения, в частности, движение по окружности и движение тела, брошенного под углом к горизонту (траектория – парабола). Основными видами движения являются равномерное и равнопеременное (в частности, равноускоренное или равнозамедленное), т.е. движение с постоянным ускорением (например, в поле силы тяжести). Таблица 1. Классификация механических движений
Равномерное движение – движение с постоянной скоростью (как по модулю, так и по направлению). Такое движение – всегда прямолинейное движение. В этом случае путь всегда равен величине перемещения S. Закон равномерного движения: (1) или (1’) Если скорость меняется (по величине или по направлению), то движение считается неравномерным. Методические указания. При ответе на вопрос «Как меняется скорость тела?» необходимо выбрать один из следующих ответов: 1) скорость меняется только по направлению (величина скорости постоянна); 2) скорость меняется только по модулю (направление постоянно); 3) скорость меняется и по модулю и по направлению; 4) скорость НЕ меняется (модуль И направление постоянны!) – в случае отрицательного ответа. Наличие нескольких способов изменения скорости обусловлено тем, что это векторная величина. Для сравнения отметим, что скалярная величина характеризуется одним параметром - числовым значением (или только модуль – неотрицательное число, или, для некоторых скаляров, модуль и знак: «плюс» или «минус» - т.е. любое действительное число). Так, проекция скорости на ось есть скалярная величина определенного знака, в отличие от величины пройденного пути. Равнопеременное движение (равноускоренное или равнозамедленное, но не только!)– движение с постоянным ускорением по следующему закону: (2)
Иначе (3) (4),. Равенства, записанные в скалярной форме, требуют учета знаков перед значениями векторных величин!. Методические указания. При записи закона движения в форме 2 направления всех векторных величин сравниваются с выбранным положительным направлением осей координат, поэтому выбор знака «+» или «-» осуществляется и перед скоростью и перед ускорением. Форма 1 соответствует выбору положительного направления в сторону самого движения (по направлению начальной скорости). Замечание. При решении задач часто очень удобно использовать формулу, являющуюся следствием исключения из формул (2) и (4) параметра t: (5) Равномерное движение по окружности – движение по окружности с постоянной по модулю скоростью. Скорость как векторная величина МЕНЯЕТСЯ, но лишь по направлению (см. выше вариант 1). Поэтому в этом случае есть ускорение – центростремительное (нормальное), зависящее от модуля линейной скорости: (6) При движении по окружности тело проходит за единицу времени некоторое расстояние вдоль траектории – определяемое линейной скоростью. В то же время тело за единицу времени поворачивается на некоторый угол – определяемый угловой скоростью. Угловая скорость (при равномерном движении по окружности!) численно равна углу поворота за единицу времени: (7) Замечание. В случае неравномерного движения по окружности необходимо говорить о мгновенном значении угловой скорости, которое находится как производная от угла поворота по времени: Частота вращения n - количество оборотов в единицу времени. За один оборот принимается поворот на угол (8) Каждой угловой величине можно поставить в соответствие величину линейную (см. табл.2): Таблица 2. Связь линейных и угловых величин
Связь линейных и угловых величин можно представить схематично: Угловая величина Например, имеем формулы: (11) и, как следствие формулы (6), получаем: (13) где R - радиус окружности, an - центростремительное ускорение. Методические указания. Если скорость меняется только по направлению, т.е. есть лишь ускорение, перпендикулярное (нормальное - от слова «нормаль») скорости, то его чаще называют центростремительным (как в случае равномерного движения по окружности). Если же имеет место изменение обоих параметров (модуля и направления), то соответственно каждому из них выделяют отдельно две составляющие ускорения: тангенциальное (касательное) ускорение аt, которое направлено вдоль скорости и характеризует быстроту изменения величины скорости, и нормальное (перпендикулярное скорости) ускорение аn, относящееся к изменению направления скорости. Тогда полное ускорение равно их векторной сумме:
Отдельную группу составляют задачи на среднюю скорость движения. О средней скорости говорят, когда в течение некоторого времени Dt значение скорости менялось. Тогда если бы тело двигалось с постоянной скоростью равной Vср, то за это время Dt оно прошло бы то же самой расстояние. Поэтому по определению имеем формулу: (14). Другими словами, введение средней скорости там, где движение явно не равномерное (истинный вид движения может быть не известен, сложен или переменчив) дает как бы первое приближение этого движения, заменяя его равномерным. Методические указания. Анализируя методы решения задач, можно отметить два случая: 1) решение «от данного к искомому» или «от начала», основано на применении типичных для данной ситуации рассуждений до тех пор, пока не придем к тому, что требуется; 2) решение «от искомого к данным» или «от конца», основано на записи формул, относящихся к искомой величине (чаще, ее определение) и постепенном выражении входящих в нее неизвестных переменных через данные задачи. Так, решение задачи, где требуется найти среднюю скорость, должно начинаться с записи формулы (14). После этого на основе условия задачи выделяются основные неизвестные и через них и данные задачи выражаются все другие неизвестные. Затем при подстановке в исходную формулу производится сокращение основных неизвестных и получается общая формула решения. Особое значение имеют вопросы, касающиеся относительности движения. В связи с этим необходимо усвоить формулу сложения скоростей и отработать ее применение на конкретных задачах. Мысленно представим ситуацию, когда два человека высказываются о движении одного и того же тела (пень на поляне): один говорит «пень движется», а другой – «пень покоится». Кто же из них прав? Оказывается правы могут быть оба спорящих: тот, кто стоит возле пня, и тот, кто едет мимо него в вагоне поезда. Приведенный выше вопрос не имеет смысла, пока не будет оговорено, относительно какого тела отсчета идет рассмотрение движения! Приходим, таким образом, к важнейшему заключению: движение и покой относительны. Кроме того, относительно и положение тела (один говорит: пень близко, а другой: пень далеко). На этом основано еще одно методическое требование, которое необходимо учитывать при записи кинематических зависимостей (в частности, законов движения): все величины, относящиеся к движению и задействованные в одной и той же расчетной формуле, должны быть заданы в одной и той же системе отсчета! Однако, анализируя конкретные ситуации, бывает просто необходимо переходить из одной системы отсчета к другой. Формула сложения скоростей позволяет согласовывать кинематические величины, заданные в двух различных системах отсчета, одна из которых неподвижна, а другая движется относительно нее с некоторой скоростью. Обозначим Т – тело, движение которого рассматривается относительно двух разных систем отсчета, К – неподвижная система отсчета, К’ – движущаяся (равномерно относительно К!) система отсчета. Пусть Формула сложения скоростей верна только в векторной форме и имеет простой вид: (15) Методические указания. Решение задач на относительность движения осуществляется 2-м способом (см. методические указания на стр. 12), т.е. начинается с записи формулы (15). (Предварительно необходимо четко выделить тройку (Т, К, К’) и соответственно «распознать» данные в задачи значения скоростей). Затем из нее выражается вектор искомой скорости, строится на основе правила «треугольника» сложения векторов «треугольник скоростей» и из него на основе геометрических соображений определяется нужная величина.
|

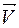 =
= 

 - равномерное движение по окружности (скорость меняется только по направлению, следовательно, тело движется с центростреми-тельным ускорением
- равномерное движение по окружности (скорость меняется только по направлению, следовательно, тело движется с центростреми-тельным ускорением  )
)
 - равнопеременное движение (в частности: равноускоренное или равнозамедленное, в общем: движение с постоянным ускорением (например, в поле тяготения Земли с ускорением свободного падения
- равнопеременное движение (в частности: равноускоренное или равнозамедленное, в общем: движение с постоянным ускорением (например, в поле тяготения Земли с ускорением свободного падения  )
)
 ,
, 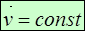 - (1-я форма), где
- (1-я форма), где  - модуль скорости,
- модуль скорости, - (2-я форма), где
- (2-я форма), где  - проекция скорости движения на ось х.
- проекция скорости движения на ось х. - зависимость пути S от времени (форма 1),
- зависимость пути S от времени (форма 1), - модуль начальной скорость, а – модуль ускорения, t – затраченный промежуток времени.
- модуль начальной скорость, а – модуль ускорения, t – затраченный промежуток времени. - зависимость координаты от времени (форма 2),
- зависимость координаты от времени (форма 2), - путь, пройденный при движении с ускорением a на участке изменения скорости от
- путь, пройденный при движении с ускорением a на участке изменения скорости от  , где R – радиус окружности.
, где R – радиус окружности. , где
, где  - угол поворота за время
- угол поворота за время  .
. . Кроме того, угловая скорость имеет и направление, которое находится по правилу правого буравчика; в частности, угловая скорость перпендикулярна плоскости вращения. Т.е. угловая скорость в общем также является векторной величиной!
. Кроме того, угловая скорость имеет и направление, которое находится по правилу правого буравчика; в частности, угловая скорость перпендикулярна плоскости вращения. Т.е. угловая скорость в общем также является векторной величиной! . Период вращения Т – время одного полного оборота. Основные формулы:
. Период вращения Т – время одного полного оборота. Основные формулы: ; (9)
; (9)  ; (10)
; (10)  .
.



 R = Линейная величина
R = Линейная величина ; (12)
; (12) 
 ,
, .
.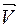 – скорость тела (Т) в К (абсолютная скорость тела, одинакова для любых неподвижных систем отсчета!),
– скорость тела (Т) в К (абсолютная скорость тела, одинакова для любых неподвижных систем отсчета!),  – скорость тела в К’ (относительная скорость, зависит от системы К’),
– скорость тела в К’ (относительная скорость, зависит от системы К’), 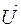 – скорость К’ относительно К.
– скорость К’ относительно К.



