Cвойства для систем с вертикальной осью :
1. Угловое неизвестное, находящееся на оси симметрии, является обратносимметричным.
2. Вертикальное линейное неизвестное, находящееся на оси симметрии, является симметричным.
3. Горизонтальное линейное неизвестное, направленное вдоль ригеля, является обратносимметричным.
Если заданная система 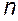 раз кинематически неопределима, то после наложения на нее
раз кинематически неопределима, то после наложения на нее  дополнительных связей, устраняющих возможные перемещения ее узлов и приложения к ним неизвестных перемещений
дополнительных связей, устраняющих возможные перемещения ее узлов и приложения к ним неизвестных перемещений  , система канонических уравнений метода перемещений для определения этих неизвестных может быть представлена в виде
, система канонических уравнений метода перемещений для определения этих неизвестных может быть представлена в виде
 (1.3)
(1.3)
или в матричной форме:
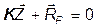 , (1.4)
, (1.4)
где 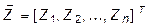 - вектор неизвестных;
- вектор неизвестных;
 - вектор свободных (грузовых) членов;
- вектор свободных (грузовых) членов;
 - матрица внешней жесткости системы, которая в развернутой форме имеет вид
- матрица внешней жесткости системы, которая в развернутой форме имеет вид
 (1.5)
(1.5)
Все реакции, обозначенные буквой  называются единичными реакциями. Так,
называются единичными реакциями. Так,  - реакция, возникающая в дополнительной связи
- реакция, возникающая в дополнительной связи  где имеется перемещение
где имеется перемещение  от перемещения связи
от перемещения связи 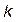 на единицу (от
на единицу (от  );
); 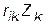 - реакция, возникающая в дополнительной связи
- реакция, возникающая в дополнительной связи  от перемещения связи
от перемещения связи  на величину
на величину  ;
;  - реакция, возникающая в дополнительной связи
- реакция, возникающая в дополнительной связи  где имеется перемещение
где имеется перемещение  от смещения этой же связи на единицу (
от смещения этой же связи на единицу ( );
);  - реакция в связи
- реакция в связи  от ее смещения на величину
от ее смещения на величину  ;
;  - реакция, возникающая в связи
- реакция, возникающая в связи 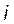 от действия на основную систему нагрузки. Первый индекс у
от действия на основную систему нагрузки. Первый индекс у  и
и 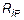 показывает номер связи, в которой возникает реакция, а второй - указывает на причину появления реакции. Реакция, возникающая в связи
показывает номер связи, в которой возникает реакция, а второй - указывает на причину появления реакции. Реакция, возникающая в связи  (
( ,
, 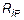 ), считается положительной, если ее направление совпадает с направлением неизвестного перемещения
), считается положительной, если ее направление совпадает с направлением неизвестного перемещения  показанного на основной системе. Еще раз напомним, что реакции, возникающие в дополнительных заделках (защемлениях), называются реактивными моментами, а в дополнительных опорных стержнях, - просто реакциями, или реактивными усилиями.
показанного на основной системе. Еще раз напомним, что реакции, возникающие в дополнительных заделках (защемлениях), называются реактивными моментами, а в дополнительных опорных стержнях, - просто реакциями, или реактивными усилиями.
Поскольку уравнения (1.3), (1.4) являются условиями эквивалентности по усилиям заданной и основной систем (условиями равновесия), ф и з и ч е с к и й с м ы с л любого  -го уравнения заключается в том, что суммарная реакция в дополнительной связи
-го уравнения заключается в том, что суммарная реакция в дополнительной связи  от действия всех неизвестных и нагрузки на основную систему равна нулю, потому что в заданной системе эта дополнительная связь отсутствует.
от действия всех неизвестных и нагрузки на основную систему равна нулю, потому что в заданной системе эта дополнительная связь отсутствует.
Как и в методе сил, коэффициенты с одинаковыми индексами, расположенные на главной диагонали матрицы  (6.5), называются г л а в н ы м и коэффициентами, которые всегда п о л о ж и- т е л ь н ы и не равны нулю. Остальные коэффициенты этой матрицы называются п о б о ч н ы м и. Они могут быть положительными, отрицательными и равными нулю. В соответствии с первой теоремой Рэлея о взаимности реакций между побочными коэффициентами выполняется соотношение
(6.5), называются г л а в н ы м и коэффициентами, которые всегда п о л о ж и- т е л ь н ы и не равны нулю. Остальные коэффициенты этой матрицы называются п о б о ч н ы м и. Они могут быть положительными, отрицательными и равными нулю. В соответствии с первой теоремой Рэлея о взаимности реакций между побочными коэффициентами выполняется соотношение
 ,
,
вследствие чего матрица внешней жесткости  будет симметричной и, как матрица внешней податливости
будет симметричной и, как матрица внешней податливости  в методе сил, положительно определенной.
в методе сил, положительно определенной.
Для вычисления коэффициентов при неизвестных и свободных членов канонических уравнений метода перемещений надо сначала построить эпюры изгибающих моментов  в основной системе от единичных неизвестных перемещений узлов рамы и
в основной системе от единичных неизвестных перемещений узлов рамы и  от внешней нагрузки. При построении единичных эпюр моментов
от внешней нагрузки. При построении единичных эпюр моментов  весьма желательно предварительно показать пунктирной линией характер деформирования оси каждого стержня от единичного угла поворота или линейного смещения, что позволит установить положение растянутых волокон и безошибочно перенести из табл. 6.1 эпюры моментов для отдельных балок на основную систему и тем самым правильно изобразить единичную эпюру моментов в целом.
весьма желательно предварительно показать пунктирной линией характер деформирования оси каждого стержня от единичного угла поворота или линейного смещения, что позволит установить положение растянутых волокон и безошибочно перенести из табл. 6.1 эпюры моментов для отдельных балок на основную систему и тем самым правильно изобразить единичную эпюру моментов в целом.
После построения единичных эпюр моментов  и грузовой эпюры моментов
и грузовой эпюры моментов  переходят к вычислению коэффициентов
переходят к вычислению коэффициентов  и свободных членов
и свободных членов  применяя статический или кинематический (перемножение эпюр) способы.
применяя статический или кинематический (перемножение эпюр) способы.
С т а т и ч е с к и й с п о с о б из-за своей простоты и наглядности является основным способом определения коэффициентов при неизвестных и свободных членов и основан на использовании уравнений равновесия. Особенно просто находятся реакции, представляющие собой реактивные моменты во введенных защемлениях, из условий равновесия вырезанных из основной системы узлов в виде 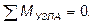
Несколько сложнее вычисляются реакции, представляющие собой реактивные усилия во введенных опорных стержнях. Для их определения составляются уравнения равновесия некоторой отсеченной части основной системы, содержащей эти силовые связи, в виде 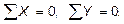
К и н е м а т и ч е с к и й с п о с о б дает возможность находить реактивные моменты и усилия в дополнительных связях аналогично тому, как это делалось в методе сил, т.е. путем интегрирования (перемножения) соответствующих эпюр по формулам, вытекающим из теоремы о взаимности работ:
 (1.6)
(1.6)
где  ,
,  – единичные эпюры моментов, построенные в основной системе метода перемещений;
– единичные эпюры моментов, построенные в основной системе метода перемещений;  – эпюра моментов от нагрузки, построенная в любой статически определимой системе, полученной из заданной.
– эпюра моментов от нагрузки, построенная в любой статически определимой системе, полученной из заданной.
В практических расчетах при определении единичных реакций и свободных членов или их проверке кинематический способ из-за трудоемкости вычислений и вероятности появления ошибок не при-меняется. Как исключение он может быть использован для вычисления некоторых коэффициентов  при расчете рам с наклонными стойками, когда применение статического способа усложняется.
при расчете рам с наклонными стойками, когда применение статического способа усложняется.
В то же время формулы (1.6) примечательны тем, что при нахождении коэффициентов уравнений (1.3) можно воспользоваться, как и в методе сил, свойством взаимной ортогональности эпюр моментов, из которого следует, что если одна из эпюр моментов симметрична, а другая – обратносимметрична, то соответствующий коэффициент  или свободный член
или свободный член  являющийся результатом перемножения этих эпюр, априорно равен нулю.
являющийся результатом перемножения этих эпюр, априорно равен нулю.
В симметричных системах разделение неизвестных перемещений  на две группы (симметричные и обратносимметричные), как известно, приводит к разделению общей системы канонических уравнений (1.3) на две подсистемы, одна из которых содержит только симметричные, а другая - только обратносимметричные неизвестные. В методе перемещений для таких систем остаются справедливыми и два правила о действии на симметричное сооружение симметричной или обратносимметричной нагрузки.
на две группы (симметричные и обратносимметричные), как известно, приводит к разделению общей системы канонических уравнений (1.3) на две подсистемы, одна из которых содержит только симметричные, а другая - только обратносимметричные неизвестные. В методе перемещений для таких систем остаются справедливыми и два правила о действии на симметричное сооружение симметричной или обратносимметричной нагрузки.
Подставив найденные коэффициенты  и свободные члены
и свободные члены  в систему (1.3) и решив ее, найдем действительные значения неизвестных метода перемещений
в систему (1.3) и решив ее, найдем действительные значения неизвестных метода перемещений  После этого окончательную эпюру моментов строим, как и в методе сил, т.е. как алгебраическую сумму эпюры от заданной нагрузки в основной системе
После этого окончательную эпюру моментов строим, как и в методе сил, т.е. как алгебраическую сумму эпюры от заданной нагрузки в основной системе  и единичных эпюр
и единичных эпюр 
 умноженных на найденные значения неизвестных:
умноженных на найденные значения неизвестных:
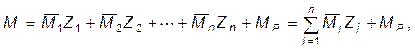
где  - исправленная единичная эпюра моментов.
- исправленная единичная эпюра моментов.
Следует отметить, что как исходные  ,
,  , так и исправленные эпюры моментов метода перемещений являются неуравновешенными, в то время как окончательная эпюра изгибающих моментов должна быть обязательно уравновешенной. Поэтому необходимым и достаточным условием правильности эпюры
, так и исправленные эпюры моментов метода перемещений являются неуравновешенными, в то время как окончательная эпюра изгибающих моментов должна быть обязательно уравновешенной. Поэтому необходимым и достаточным условием правильности эпюры  является равенство нулю реакций во всех введенных связях при правильных единичных и грузовой эпюрах. Это означает, что все узлы системы должны быть уравновешены, и должны отсутствовать реактивные усилия в дополнительных опорных стержнях. Обычно второе условие (равенство нулю реактивных усилий) сразу не проверяется, а совмещается с проверкой эпюр
является равенство нулю реакций во всех введенных связях при правильных единичных и грузовой эпюрах. Это означает, что все узлы системы должны быть уравновешены, и должны отсутствовать реактивные усилия в дополнительных опорных стержнях. Обычно второе условие (равенство нулю реактивных усилий) сразу не проверяется, а совмещается с проверкой эпюр  и
и 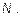
Наряду со статической может быть применена и кинематическая проверка, как это делалось в методе сил. Для этого надо окончательную эпюру моментов умножить на единичные эпюры или на их суммарную, построенные в любой основной системе метода сил, образованной из заданной. При практических расчетах эту проверку, как правило, не выполняют.
После частичной или полной проверки эпюры  по обычным правилам строят эпюры поперечных
по обычным правилам строят эпюры поперечных  и продольных сил
и продольных сил 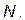
Окончательной проверкой правильности всего расчета является одновременное выполнение всех трех уравнений статики ( ) как для заданной системы в целом, так и для любых отдельных ее частей.
) как для заданной системы в целом, так и для любых отдельных ее частей.
Последовательность расчета статически неопределимых систем методом перемещений остается такой же, как и методом сил.

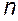 раз кинематически неопределима, то после наложения на нее
раз кинематически неопределима, то после наложения на нее  дополнительных связей, устраняющих возможные перемещения ее узлов и приложения к ним неизвестных перемещений
дополнительных связей, устраняющих возможные перемещения ее узлов и приложения к ним неизвестных перемещений  , система канонических уравнений метода перемещений для определения этих неизвестных может быть представлена в виде
, система канонических уравнений метода перемещений для определения этих неизвестных может быть представлена в виде (1.3)
(1.3)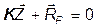 , (1.4)
, (1.4)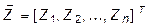 - вектор неизвестных;
- вектор неизвестных; - вектор свободных (грузовых) членов;
- вектор свободных (грузовых) членов; - матрица внешней жесткости системы, которая в развернутой форме имеет вид
- матрица внешней жесткости системы, которая в развернутой форме имеет вид (1.5)
(1.5) называются единичными реакциями. Так,
называются единичными реакциями. Так,  - реакция, возникающая в дополнительной связи
- реакция, возникающая в дополнительной связи  где имеется перемещение
где имеется перемещение  от перемещения связи
от перемещения связи 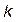 на единицу (от
на единицу (от  );
); 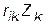 - реакция, возникающая в дополнительной связи
- реакция, возникающая в дополнительной связи  от перемещения связи
от перемещения связи  на величину
на величину  ;
;  - реакция, возникающая в дополнительной связи
- реакция, возникающая в дополнительной связи  от смещения этой же связи на единицу (
от смещения этой же связи на единицу ( );
);  - реакция в связи
- реакция в связи  от ее смещения на величину
от ее смещения на величину  ;
;  - реакция, возникающая в связи
- реакция, возникающая в связи 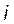 от действия на основную систему нагрузки. Первый индекс у
от действия на основную систему нагрузки. Первый индекс у  и
и 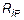 показывает номер связи, в которой возникает реакция, а второй - указывает на причину появления реакции. Реакция, возникающая в связи
показывает номер связи, в которой возникает реакция, а второй - указывает на причину появления реакции. Реакция, возникающая в связи  (6.5), называются г л а в н ы м и коэффициентами, которые всегда п о л о ж и- т е л ь н ы и не равны нулю. Остальные коэффициенты этой матрицы называются п о б о ч н ы м и. Они могут быть положительными, отрицательными и равными нулю. В соответствии с первой теоремой Рэлея о взаимности реакций между побочными коэффициентами выполняется соотношение
(6.5), называются г л а в н ы м и коэффициентами, которые всегда п о л о ж и- т е л ь н ы и не равны нулю. Остальные коэффициенты этой матрицы называются п о б о ч н ы м и. Они могут быть положительными, отрицательными и равными нулю. В соответствии с первой теоремой Рэлея о взаимности реакций между побочными коэффициентами выполняется соотношение ,
, в методе сил, положительно определенной.
в методе сил, положительно определенной. в основной системе от единичных неизвестных перемещений узлов рамы и
в основной системе от единичных неизвестных перемещений узлов рамы и  от внешней нагрузки. При построении единичных эпюр моментов
от внешней нагрузки. При построении единичных эпюр моментов  и грузовой эпюры моментов
и грузовой эпюры моментов  переходят к вычислению коэффициентов
переходят к вычислению коэффициентов  и свободных членов
и свободных членов  применяя статический или кинематический (перемножение эпюр) способы.
применяя статический или кинематический (перемножение эпюр) способы.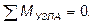
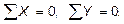
 (1.6)
(1.6) – единичные эпюры моментов, построенные в основной системе метода перемещений;
– единичные эпюры моментов, построенные в основной системе метода перемещений;  – эпюра моментов от нагрузки, построенная в любой статически определимой системе, полученной из заданной.
– эпюра моментов от нагрузки, построенная в любой статически определимой системе, полученной из заданной. при расчете рам с наклонными стойками, когда применение статического способа усложняется.
при расчете рам с наклонными стойками, когда применение статического способа усложняется. или свободный член
или свободный член  на две группы (симметричные и обратносимметричные), как известно, приводит к разделению общей системы канонических уравнений (1.3) на две подсистемы, одна из которых содержит только симметричные, а другая - только обратносимметричные неизвестные. В методе перемещений для таких систем остаются справедливыми и два правила о действии на симметричное сооружение симметричной или обратносимметричной нагрузки.
на две группы (симметричные и обратносимметричные), как известно, приводит к разделению общей системы канонических уравнений (1.3) на две подсистемы, одна из которых содержит только симметричные, а другая - только обратносимметричные неизвестные. В методе перемещений для таких систем остаются справедливыми и два правила о действии на симметричное сооружение симметричной или обратносимметричной нагрузки. После этого окончательную эпюру моментов строим, как и в методе сил, т.е. как алгебраическую сумму эпюры от заданной нагрузки в основной системе
После этого окончательную эпюру моментов строим, как и в методе сил, т.е. как алгебраическую сумму эпюры от заданной нагрузки в основной системе  и единичных эпюр
и единичных эпюр 
 умноженных на найденные значения неизвестных:
умноженных на найденные значения неизвестных: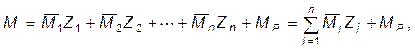
 - исправленная единичная эпюра моментов.
- исправленная единичная эпюра моментов. ,
,  является равенство нулю реакций во всех введенных связях при правильных единичных и грузовой эпюрах. Это означает, что все узлы системы должны быть уравновешены, и должны отсутствовать реактивные усилия в дополнительных опорных стержнях. Обычно второе условие (равенство нулю реактивных усилий) сразу не проверяется, а совмещается с проверкой эпюр
является равенство нулю реакций во всех введенных связях при правильных единичных и грузовой эпюрах. Это означает, что все узлы системы должны быть уравновешены, и должны отсутствовать реактивные усилия в дополнительных опорных стержнях. Обычно второе условие (равенство нулю реактивных усилий) сразу не проверяется, а совмещается с проверкой эпюр  и
и 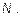
 и продольных сил
и продольных сил 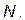
 ) как для заданной системы в целом, так и для любых отдельных ее частей.
) как для заданной системы в целом, так и для любых отдельных ее частей.


