Основная система метода перемещений при расчете рам и балок на кинематическое воздействие (чаще всего на осадку опор) остается такой же, как и при расчете на силовое и тепловое воздействия. Канонические уравнения для  раз кинематически неопределимых систем отличаются от систем уравнений (1.3), (1.10) только свободными членами и записываются в виде
раз кинематически неопределимых систем отличаются от систем уравнений (1.3), (1.10) только свободными членами и записываются в виде
 (1.15)
(1.15)
Физический смысл любого  - го уравнения системы (1.15) аналогичен тому, как он формулировался при других воздействиях. Свободные члены канонических уравнений
- го уравнения системы (1.15) аналогичен тому, как он формулировался при других воздействиях. Свободные члены канонических уравнений  – реакции во введенных дополнительных связях от кинематического воздействия. Для их вычисления нужно построить в основной системе грузовую эпюру
– реакции во введенных дополнительных связях от кинематического воздействия. Для их вычисления нужно построить в основной системе грузовую эпюру  от заданного смещения опор.
от заданного смещения опор.
Прежде чем строить эпюру  надо в основной системе показать новое положение узлов, вызванное смещением опор, изобразить деформации стержней и определить относительные поступательные перемещения их концов по перпендикулярному к ним направлению. Эта процедура аналогична той, которая применялась при построении эпюры
надо в основной системе показать новое положение узлов, вызванное смещением опор, изобразить деформации стержней и определить относительные поступательные перемещения их концов по перпендикулярному к ним направлению. Эта процедура аналогична той, которая применялась при построении эпюры  от равномерного нагрева. После этого эпюра
от равномерного нагрева. После этого эпюра  весьма просто строится путем перенесения на деформированные стержни основной системы соответствующих эпюр моментов из табл. 1.1, ординаты которых нужно умножить на найденные значения взаимных смещений концов стержней.
весьма просто строится путем перенесения на деформированные стержни основной системы соответствующих эпюр моментов из табл. 1.1, ординаты которых нужно умножить на найденные значения взаимных смещений концов стержней.
Определив все коэффициенты, входящие в систему канонических уравнений и решив ее, окончательную эпюру изгибающих моментов в заданной системе от смещения опор можно построить по формуле
 (1.17)
(1.17)
Помимо обычной проверки правильности окончательной эпюры  (равенство нулю реакций во введенных связях) можно использовать формулу (1.14).
(равенство нулю реакций во введенных связях) можно использовать формулу (1.14).
Если решение задачи ведется с точностью до масштабного множителя 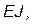 то числа получаются малыми, поэтому, чтобы избежать больших расхождений в окончательных значениях моментов в узлах, необходимо учитывать при расчете большое число знаков после запятой (как минимум 5 знаков).
то числа получаются малыми, поэтому, чтобы избежать больших расхождений в окончательных значениях моментов в узлах, необходимо учитывать при расчете большое число знаков после запятой (как минимум 5 знаков).
Последовательность расчета систем на заданное смещение опор остается прежней.

 раз кинематически неопределимых систем отличаются от систем уравнений (1.3), (1.10) только свободными членами и записываются в виде
раз кинематически неопределимых систем отличаются от систем уравнений (1.3), (1.10) только свободными членами и записываются в виде (1.15)
(1.15) - го уравнения системы (1.15) аналогичен тому, как он формулировался при других воздействиях. Свободные члены канонических уравнений
- го уравнения системы (1.15) аналогичен тому, как он формулировался при других воздействиях. Свободные члены канонических уравнений  – реакции во введенных дополнительных связях от кинематического воздействия. Для их вычисления нужно построить в основной системе грузовую эпюру
– реакции во введенных дополнительных связях от кинематического воздействия. Для их вычисления нужно построить в основной системе грузовую эпюру  от заданного смещения опор.
от заданного смещения опор. надо в основной системе показать новое положение узлов, вызванное смещением опор, изобразить деформации стержней и определить относительные поступательные перемещения их концов по перпендикулярному к ним направлению. Эта процедура аналогична той, которая применялась при построении эпюры
надо в основной системе показать новое положение узлов, вызванное смещением опор, изобразить деформации стержней и определить относительные поступательные перемещения их концов по перпендикулярному к ним направлению. Эта процедура аналогична той, которая применялась при построении эпюры  от равномерного нагрева. После этого эпюра
от равномерного нагрева. После этого эпюра  весьма просто строится путем перенесения на деформированные стержни основной системы соответствующих эпюр моментов из табл. 1.1, ординаты которых нужно умножить на найденные значения взаимных смещений концов стержней.
весьма просто строится путем перенесения на деформированные стержни основной системы соответствующих эпюр моментов из табл. 1.1, ординаты которых нужно умножить на найденные значения взаимных смещений концов стержней. (1.17)
(1.17) (равенство нулю реакций во введенных связях) можно использовать формулу (1.14).
(равенство нулю реакций во введенных связях) можно использовать формулу (1.14).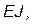 то числа получаются малыми, поэтому, чтобы избежать больших расхождений в окончательных значениях моментов в узлах, необходимо учитывать при расчете большое число знаков после запятой (как минимум 5 знаков).
то числа получаются малыми, поэтому, чтобы избежать больших расхождений в окончательных значениях моментов в узлах, необходимо учитывать при расчете большое число знаков после запятой (как минимум 5 знаков).


