| 1.2. Тепловое воздействие
|
Канонические уравнения метода перемещений для  раз кинематически неопределимых систем при расчете на тепловое воздействие отличаются от системы уравнений (6.3) только свободными членами и записываются в виде
раз кинематически неопределимых систем при расчете на тепловое воздействие отличаются от системы уравнений (6.3) только свободными членами и записываются в виде
 (1.7)
(1.7)
Физический смысл любого  -го уравнения системы (1.7) заключается в отсутствии (равенстве нулю) суммарной реакции в дополнительной связи
-го уравнения системы (1.7) заключается в отсутствии (равенстве нулю) суммарной реакции в дополнительной связи  от действия на основную систему неизвестных и тепловой нагрузки, так как в заданной системе этой дополнительной связи нет. Основная система метода перемещений здесь, естественно, остается той же, что и при расчете на силовое воздействие. Как и ранее, будем предполагать, что температура постоянна по длине каждого стержня, а по толщине нагреваемого элемента - изменяется по линейному закону. В этом случае температура по оси стержня (равномерный нагрев) определяется как
от действия на основную систему неизвестных и тепловой нагрузки, так как в заданной системе этой дополнительной связи нет. Основная система метода перемещений здесь, естественно, остается той же, что и при расчете на силовое воздействие. Как и ранее, будем предполагать, что температура постоянна по длине каждого стержня, а по толщине нагреваемого элемента - изменяется по линейному закону. В этом случае температура по оси стержня (равномерный нагрев) определяется как  , а разность (перепад) температур
, а разность (перепад) температур  (неравномерный нагрев) – как
(неравномерный нагрев) – как  .
.
Чтобы вычислить свободные члены  , необходимо построить в статически неопределимой основной системе метода перемещений грузовую эпюру моментов
, необходимо построить в статически неопределимой основной системе метода перемещений грузовую эпюру моментов  от теплового воздействия. Эта эпюра будет состоять из суммы двух эпюр моментов: эпюры
от теплового воздействия. Эта эпюра будет состоять из суммы двух эпюр моментов: эпюры 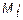 от неравномерного нагрева стержней и эпюры
от неравномерного нагрева стержней и эпюры  от равномерного нагрева стержней, т.е.
от равномерного нагрева стержней, т.е.
 (1.8)
(1.8)
Эпюра 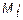 весьма просто строится в основной системе при помощи п. 9 и 18 табл. 1.1. Построение эпюры
весьма просто строится в основной системе при помощи п. 9 и 18 табл. 1.1. Построение эпюры 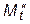 несколько сложнее. Для этого надо знать взаимные перемещения концов каждого стержня
несколько сложнее. Для этого надо знать взаимные перемещения концов каждого стержня  по перпендикулярному к его оси направлению. В результате равномерного нагрева стержни основной системы удлинятся или укоротятся, а ее узлы, не поворачиваясь, получат поступательные перемещения и займут новое положение, вследствие чего стержни системы искривятся и в них возникнут изгибающие моменты. Удлинение или укорочение
по перпендикулярному к его оси направлению. В результате равномерного нагрева стержни основной системы удлинятся или укоротятся, а ее узлы, не поворачиваясь, получат поступательные перемещения и займут новое положение, вследствие чего стержни системы искривятся и в них возникнут изгибающие моменты. Удлинение или укорочение  -го стержня основной системы определяется по известной из школьного курса физики формуле:
-го стержня основной системы определяется по известной из школьного курса физики формуле:
 (1.9)
(1.9)
где  – коэффициент линейного расширения материала;
– коэффициент линейного расширения материала;
 – длина нагреваемого стержня.
– длина нагреваемого стержня.
Из приведенных выше рассуждений следует, что для построения эпюры  нужно сначала на отдельном рисунке показать новое положение узлов основной системы с величинами их смещений и изобразить деформации искривленных стержней. После этого в новой схеме основной системы переносим на деформированные стержни эпюры моментов с п. 2 и 13 табл. 1.1, ординаты которых надо умножить на соответствующие значения
нужно сначала на отдельном рисунке показать новое положение узлов основной системы с величинами их смещений и изобразить деформации искривленных стержней. После этого в новой схеме основной системы переносим на деформированные стержни эпюры моментов с п. 2 и 13 табл. 1.1, ординаты которых надо умножить на соответствующие значения 
Так, для балки, защемленной на одном конце и шарнирно опертой на другом, эпюра моментов представляет собой треугольник с ординатой в защемлении, равной
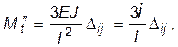 (1.10)
(1.10)
а для балки, защемленной с двух концов, эпюра моментов будет представлять собой равнобокую перекрученную трапецию с моментами по концам, равными
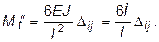 (1.11)
(1.11)
Напомним, что  – взаимное перемещение концов каждого стержня в основной системе по направлению, перпендикулярному к оси стержня.
– взаимное перемещение концов каждого стержня в основной системе по направлению, перпендикулярному к оси стержня.
Полученная таким образом эпюра моментов и есть эпюра 
Окончательная грузовая эпюра 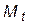 в основной системе строится по формуле (1.8).
в основной системе строится по формуле (1.8).
Заметим, что свободные члены  можно вычислить не только по единой эпюре
можно вычислить не только по единой эпюре  , но и отдельно с помощью эпюр
, но и отдельно с помощью эпюр  и
и 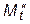 по следующей формуле:
по следующей формуле:
 (1.12)
(1.12)
где  – реакция во введенной связи
– реакция во введенной связи  от неравномерного нагрева, а
от неравномерного нагрева, а  – реакция в той же связи от равномерного нагрева.
– реакция в той же связи от равномерного нагрева.
После вычисления всех коэффициентов, решения системы канонических уравнений и нахождения неизвестных  окончательная эпюра изгибающих моментов для заданной системы строится по формуле
окончательная эпюра изгибающих моментов для заданной системы строится по формуле
 (1.13)
(1.13)
Наряду с обычными проверками окончательной эпюры моментов, полученной в результате расчета заданной системы методом перемещений на тепловое воздействие (равенство нулю реакций во введенных связях), возможна проверка перемножением окончательной эпюры  с любой единичной
с любой единичной  или суммарной единичной эпюрой
или суммарной единичной эпюрой 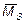 , построенными в основной системе метода перемещений:
, построенными в основной системе метода перемещений:
 (1.14)
(1.14)
Равенства (6.17) следуют из теоремы Бетти о взаимности работ.
Последовательность расчета систем при тепловом воздействии сохраняется такой же, как и при силовом воздействии.
Если в задачах (примерах) толщина нагреваемых элементов не указана, то ее следует принимать для всех элементов равной  м.
м.
| Кинематическое воздействие
|

 раз кинематически неопределимых систем при расчете на тепловое воздействие отличаются от системы уравнений (6.3) только свободными членами и записываются в виде
раз кинематически неопределимых систем при расчете на тепловое воздействие отличаются от системы уравнений (6.3) только свободными членами и записываются в виде (1.7)
(1.7) -го уравнения системы (1.7) заключается в отсутствии (равенстве нулю) суммарной реакции в дополнительной связи
-го уравнения системы (1.7) заключается в отсутствии (равенстве нулю) суммарной реакции в дополнительной связи  , а разность (перепад) температур
, а разность (перепад) температур  (неравномерный нагрев) – как
(неравномерный нагрев) – как  .
. , необходимо построить в статически неопределимой основной системе метода перемещений грузовую эпюру моментов
, необходимо построить в статически неопределимой основной системе метода перемещений грузовую эпюру моментов  от теплового воздействия. Эта эпюра будет состоять из суммы двух эпюр моментов: эпюры
от теплового воздействия. Эта эпюра будет состоять из суммы двух эпюр моментов: эпюры 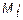 от неравномерного нагрева стержней и эпюры
от неравномерного нагрева стержней и эпюры  от равномерного нагрева стержней, т.е.
от равномерного нагрева стержней, т.е. (1.8)
(1.8)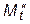 несколько сложнее. Для этого надо знать взаимные перемещения концов каждого стержня
несколько сложнее. Для этого надо знать взаимные перемещения концов каждого стержня  по перпендикулярному к его оси направлению. В результате равномерного нагрева стержни основной системы удлинятся или укоротятся, а ее узлы, не поворачиваясь, получат поступательные перемещения и займут новое положение, вследствие чего стержни системы искривятся и в них возникнут изгибающие моменты. Удлинение или укорочение
по перпендикулярному к его оси направлению. В результате равномерного нагрева стержни основной системы удлинятся или укоротятся, а ее узлы, не поворачиваясь, получат поступательные перемещения и займут новое положение, вследствие чего стержни системы искривятся и в них возникнут изгибающие моменты. Удлинение или укорочение  (1.9)
(1.9) – коэффициент линейного расширения материала;
– коэффициент линейного расширения материала; – длина нагреваемого стержня.
– длина нагреваемого стержня. нужно сначала на отдельном рисунке показать новое положение узлов основной системы с величинами их смещений и изобразить деформации искривленных стержней. После этого в новой схеме основной системы переносим на деформированные стержни эпюры моментов с п. 2 и 13 табл. 1.1, ординаты которых надо умножить на соответствующие значения
нужно сначала на отдельном рисунке показать новое положение узлов основной системы с величинами их смещений и изобразить деформации искривленных стержней. После этого в новой схеме основной системы переносим на деформированные стержни эпюры моментов с п. 2 и 13 табл. 1.1, ординаты которых надо умножить на соответствующие значения 
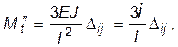 (1.10)
(1.10)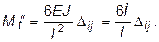 (1.11)
(1.11)
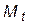 в основной системе строится по формуле (1.8).
в основной системе строится по формуле (1.8). можно вычислить не только по единой эпюре
можно вычислить не только по единой эпюре  , но и отдельно с помощью эпюр
, но и отдельно с помощью эпюр  и
и  (1.12)
(1.12) – реакция во введенной связи
– реакция во введенной связи  – реакция в той же связи от равномерного нагрева.
– реакция в той же связи от равномерного нагрева. окончательная эпюра изгибающих моментов для заданной системы строится по формуле
окончательная эпюра изгибающих моментов для заданной системы строится по формуле (1.13)
(1.13) с любой единичной
с любой единичной  или суммарной единичной эпюрой
или суммарной единичной эпюрой 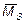 , построенными в основной системе метода перемещений:
, построенными в основной системе метода перемещений: (1.14)
(1.14) м.
м.


