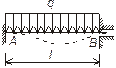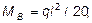Основные гипотезы метода перемещений
1. Как и в методе сил, пренебрегаем влиянием продольных и поперечных сил на деформации стержней, т.е. учитываем только деформации изгиба. 2. Поскольку все перемещения принимаются малыми, то можно пренебречь сближением концов стержня при его изгибе, т.е. предполагается, что первоначальная длина Из этих гипотез следует, что 6.1. Силовое воздействие
Общее число неизвестных метода перемещений называют с т е- п е н ь ю к и н е м а т и ч е с к о й н е о п р е д е л и м о с т и с и с т е м ы и обозначают буквой
Число неизвестных углов поворота Число независимых линейных смещений узлов
где У – число шарнирных узлов рамы, включая опорные; С – число стержней рамы; С 0 – число опорных связей. По шарнирной схеме можно определить не только количество линейных смещений, но и их направления. Определим число неизвестных метода перемещений для некоторых систем.
Рис.1.2 Возможно только горизонтальное смещение ригеля. Степень кинематической неопределимости составляет
Для рамы, изображенной на рис. 1.3, а, имеем
Возможны горизонтальные смещения узлов
Рис.1.3 Порядок расчета сооружения методом перемещений аналогичен порядку расчета стержневых систем методом сил. Подсчитав степень кинематической неопределимости системы, вводят в расчет вместо заданной системы основную, но получают ее здесь не отбрасыванием лишних связей, а наложением дополнительных, устраняющих возможные перемещения узлов. Если во все жесткие узлы системы ввести заделки (защемления), препятствующие поворотам узлов, и закрепить узлы от поступательных смещений установкой дополнительных стержней (опорных стержней), то получим в качестве основной системы совокупность независимых однопролетных статически неопределимых балок двух видов: балка с двумя заделками по концам и балка, у которой на одном конце заделка, а на другом – шарнирно-подвижная опора. Эти балки постоянного сечения заранее рассчитаны на все виды воздействий (см., например, задачи для самостоятельного решения в гл. 5 и ответы к ним), и их решения для наиболее часто встречающихся случаев помещены в табл. 1.1. С помощью табл. 1.1 в дальнейшем весьма просто строятся единичные и грузовые эпюры моментов путем формального переноса соответствующих эпюр моментов из таблицы на деформированные стержни основной системы от различных воздействий. Число вводимых связей равно степени кинематической неопределимости системы: число дополнительных заделок совпадает со степенью угловой подвижности (количество жестких узлов Дополнительная заделка эквивалентна одной связи и отличается от обычной опорной жесткой заделки, которая эквивалентна трем связям, тем, что препятствует только угловым перемещениям узлов и не препятствует их поступательным перемещениям. В дополнительной заделке может возникать в качестве реакции только момент. Эта так называемая моментная, или угловая связь. В дополнительном стержне возникает реакция, направленная по оси этого стержня, – это силовая или поступательная связь. Поскольку узлы заданной системы под внешним воздействием могли иметь угловые и линейные перемещения, а в основной системе они невозможны, чтобы сделать основную систему эквивалентной заданной по перемещениям и усилиям, надо дополнительно к заданному внешнему воздействию приложить во введенные связи действительные угловые и линейные перемещения, которые пока неизвестны. Этими перемещениями компенсируется введение дополнительных закреплений, и как раз они являются основными неизвестными метода перемещений, которые обозначаются буквой При расчете симметричных систем методом перемещений, так же, как и при расчете методом сил, можно и нужно применять способ группировки неизвестных, который значительно облегчает расчет. Таблица 1.1
Неизвестные перемещения симметрично расположенных узлов группируются в новые парные неизвестные, представляющие собой симметричные и обратносимметричные перемещения. Группировать можно как угловые, так и линейные неизвестные. В расчетной практике чаще встречаются задачи, в которых группируются только угловые неизвестные. Тогда угол поворота одного узла представляем как сумму двух неодинаковых в общем случае углов, а угол поворота симметричного узла – как их разность. За одно из неизвестных принимается теперь поворот уже не одного, а сразу двух симметрично расположенных узлов на одну и ту же величину и в одном направлении. Поворот этих же узлов на одну и ту же величину в противоположных направлениях принимается за второе групповое неизвестное.
|

 прямого стержня
прямого стержня  (см. рис. 1.1, а) до деформации равна длине
(см. рис. 1.1, а) до деформации равна длине  хорды
хорды  стягивающей концы стержня после его деформации (рис. 1.1, в).
стягивающей концы стержня после его деформации (рис. 1.1, в).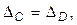 а точки
а точки  и
и  будут перемещаться перпендикулярно к стойкам
будут перемещаться перпендикулярно к стойкам  и
и  по отрезкам касательных, проведенных к окружностям радиусов
по отрезкам касательных, проведенных к окружностям радиусов  и
и  т.е. по горизонтали, и не могут иметь вертикальных перемещений. Такие же горизонтальные перемещения (
т.е. по горизонтали, и не могут иметь вертикальных перемещений. Такие же горизонтальные перемещения ( ) имеют и все остальные точки стержня
) имеют и все остальные точки стержня 
 Она определяется как сумма неизвестных углов поворота
Она определяется как сумма неизвестных углов поворота  и неизвестных независимых линейных перемещений узлов
и неизвестных независимых линейных перемещений узлов  :
: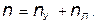 (6.1)
(6.1) Так как рама имеет два жестких узла (рис 1.2, а),
Так как рама имеет два жестких узла (рис 1.2, а),  По шарнирной схеме (рис. 1, б) определяем
По шарнирной схеме (рис. 1, б) определяем 

 Число
Число 


 Общее число неизвестных равно
Общее число неизвестных равно 
 ), а число дополнительных опорных стержней – со степенью линейной подвижности узлов
), а число дополнительных опорных стержней – со степенью линейной подвижности узлов  (
( с подстрочным индексом (
с подстрочным индексом ( ). Введением неизвестных перемещений в дополнительные связи и определяется окончательная основная система, которую можно назвать к и н е м а т и ч е с к и о п р е д е л и м о й. В дальнейшем изложении она будет изображаться с заданными нагрузками, дополнительными связями и неизвестными перемещениями
). Введением неизвестных перемещений в дополнительные связи и определяется окончательная основная система, которую можно назвать к и н е м а т и ч е с к и о п р е д е л и м о й. В дальнейшем изложении она будет изображаться с заданными нагрузками, дополнительными связями и неизвестными перемещениями  Отметим, что основная система метода перемещений – единственная.
Отметим, что основная система метода перемещений – единственная.

 – погонная жесткость
– погонная жесткость










 при
при 


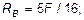



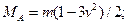
 при
при 





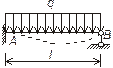


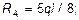

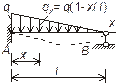




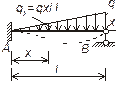








 -коэффициент линейного расширения;
-коэффициент линейного расширения;
 -высота поперечного сечения
-высота поперечного сечения



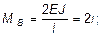

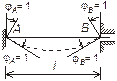











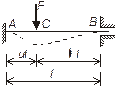
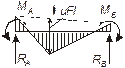

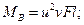

 при
при  ;
;





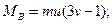
 при
при