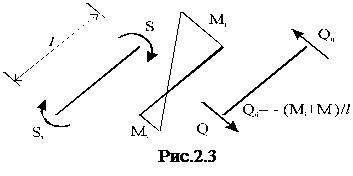Лекция№12
МАТРИЧНЫЙ МЕТОД ПЕРЕМЕЩЕНИЙ
Расчетная схема. Основная система
В учебных пособиях [9], [10], а также в учебнике [5] и задачнике [2] дано подробное изложение матричного метода перемещений и логически вытекающего из него метода конечных элементов стержневых систем, впервые предложенных автором в курсе лекций для преподавателей кафедры строительной механики МИСИ в 1979-80 учебном году. С тех пор вместе с учебными комплексами STAN-RADIUS эти издания являются основой для внедрения численных методов в учебный процесс на кафедре строительной механики в МИСИ-МГСУ. Примем, как и в классическом методе перемещений, следующие гипотезы: 1. Деформации растяжения-сжатия и сдвига малы по сравнению с деформациями изгиба, и ими можно пренебречь, т.е. считать, что перемещения узлов происходит только за счет изгиба стержней. 2. Перемещения системы малы, поэтому пренебрегаем сближением концов стержней при изгибе, т.е. длина стержня остается равной длине хорды, соединяющей его концы после искривления. 3.В шарнирно-стержневых системах (фермах) деформации растяжения-сжатия учитываются, как единственные. Сначала мы рассмотрим ММП на примерах плоской фермы и рамы, затем покажем, что предложенный алгоритм может быть распространен на любые стержневые системы, расположенные в плоскости или в пространстве. Расчетная схема ММП строится аналогично основной системе метода перемещений, где за неизвестные принимаются перемещения узлов Zi – углы поворота жестких узлов и возможные линейные перемещения узлов системы. Число неизвестных n определяется по известной формуле n = nу + nл, где nу и nл соответственно число неизвестных угловых и линейных перемещений узлов системы. Расчет производится на внешнюю нагрузку Pi – моменты и силы, приложенные в узлах по направлению возможных перемещений Zi. Если имеется внеузловая нагрузка, а также внешнее воздействие, как тепловое или осадка опор, то все эти нагрузки приводят сначала к эквивалентной узловой нагрузке. В результате расчета находятся усилия Si в стержневых элементах. В фермах – осевые усилия, в рамах – моменты по концам стержней. Кроме того, попутно определяются перемещения Zi всех узлов системы, поэтому становится известно поле перемещений конструкции в целом. Составим расчетную схему ММП фермы, показанной на рис.2.1, а.
Цифры возле стержней обозначают соответствующие индексы усилий S1 – S5, а также деформаций стержней е1 – е5. Условимся считать положительными усилия растяжения, а деформации – удлинения.
ак и в классическом методе перемещений, в раме будет 2 неизвестных – поворот жесткого узла Z1 и линейное перемещение обоих узлов по горизонтали Z2. Эти перемещения и обозначены стрелками на расчетной схеме ММП - рис. 2.2, б. Здесь связи, закрепляющие узлы от возможных перемещений, условно не показаны. Если бы нагрузка была приложена только в узлах, то вектор Р составлялся бы так же просто, как и для ферм. При действии внеузловой нагрузки ее необходимо привести к эквивалентной узловой, используя грузовые эпюры однопролетных балок для метода перемещений.
Цифры возле концевых сечений стержней обозначают неизвестные усилия – моменты S1 – S4, а также деформации поворота стержней е1 – е4 . Условимся положительными моментами считать моменты, вращающие элемент по часовой стрелке. Кстати, такое же правило принято и в программах STAN-RADIUS. Графически это правило показано на рис. 2.3. Очевидно, что в этом случае в стержне возникает отрицательная поперечная сила Qij = - (Mi + Mj)/l, вращающая элемент против часовой стрелки.
|

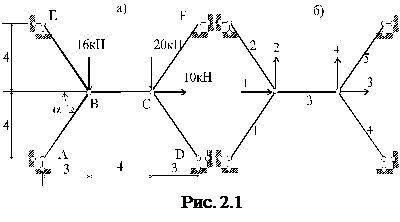
 Каждый шарнирный узел имеет 2 степени свободы на плоскости, поэтому на расчетной схеме ММП рис.1.1, б стрелками 1 – 4 показаны возможные перемещения Z1 – Z4, а также возможные внешние силы Р1 – Р4. Направление стрелок выбирается произвольно. Сопоставив их с заданными силами, составим вектор Р = [0 –16 10 –20] T. Здесь знак транспонирования означает, что вектор Р – вектор-столбец.
Каждый шарнирный узел имеет 2 степени свободы на плоскости, поэтому на расчетной схеме ММП рис.1.1, б стрелками 1 – 4 показаны возможные перемещения Z1 – Z4, а также возможные внешние силы Р1 – Р4. Направление стрелок выбирается произвольно. Сопоставив их с заданными силами, составим вектор Р = [0 –16 10 –20] T. Здесь знак транспонирования означает, что вектор Р – вектор-столбец. Составим расчетную схему ММП рамы, показанной на рис.2.2, а.
Составим расчетную схему ММП рамы, показанной на рис.2.2, а.