Лекции №18. Теорема о единственности решения (сформулировал Саймондс)
Теорема о единственности решения (сформулировал Саймондс). Является синтезом первых двух, устанавливающих пределы снизу и сверху для разрушающей нагрузки и может быть сформулирована так: Если для заданной системы и схемы загружения существует статически допустимое поле распределения моментов, причём моменты в поперечных сечениях, равные Мпл , образовались в числе точек, достаточных для того, чтобы вся система или какая-либо её часть превратились в механизм, то соответствующая этому распределения моментов нагрузка является действительно разрушающей. Необходимо подчеркнуть, что эта теорема говорит о статически допустимом (а не кинеатически допустимом) поле, т.е. условия неразрывности могут и не выполняться, что имеет место, например, при частичном разрушении. Другими словами, упругий расчёт, в котором используются и статические и геометрические уравнения, не надо! при построении статически допустимого поля; позже на примерах будет показано, что упругий расчёт для построения статически допустимого поля непригоден (при частичном разрушении). Решение задач пластического расчёта осуществляется с использованием этих трех теорем – статическим и кинематическим методами. О статическом методе мы уже говорили. Он трудоёмок и мы им практически пользоваться не будем. Рассмотрим кинематический метод. Он основан на кинематической теореме и проверяется теоремой о единственности. Для каждого возможного механизма разрушения записываем уравнение равновесия в форме работ всех внешних и внутренних сил на тех перемещениях, которые оказываются возможными для данного механизма после образования пластических шарниров. При этом работа внешних сил Рi считается положительной и равной полному произведению силы на соответствующее перемещение, т.к. возможная работа (силы считаются при этом постоянными), а работа внутренних сил, те. предельных изгибающих моментов Мпл , возникающих в пластических шарнирах отрицательной и равной произведению Мпл на угол поворота (отрицательна, т.к. внутренние силы препятствуют деформациям – противоположны по направлениям углам поворота). Это можно записать так:
Т.к. все линейные δ i угловые θ к перемещения могут быть выражены через один параметр θ (в силу малости перемещений). На него можно сократить все уравнения и найти предельную нагрузку, если все предельные несущие способности (Мпл или W пл) заданы. Наименьшая нагрузка является истинной (искомой). Распределённые нагрузки, приложенные к отдельным прямолинейным участкам, при подсчёте работ могут быть заменены их равнодействующими. Если три пластических шарнира образуются в одном пролёте получим механизм – они м.б. в сечениях с max моментами, т.е. под силой и в заделках. Пример 1. при внешней нагрузке, равномерно распределённой на каком – то участке, её работа равна работе равнодействующей силы.
Уравнение равновесия: сократив на α, получим:
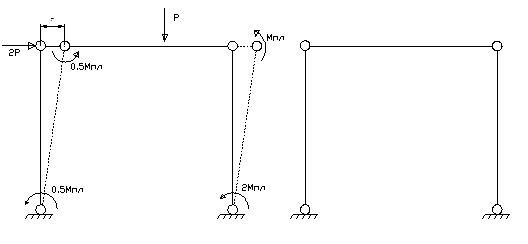
Пример 2. Рама с разными Mпл. Три лишних связи. Возможные схемы разрушения:
а.) частичное. 3 шарнира. 3 пластических шарнира в пролёте, при этом надо смотреть какие изгибающие моменты действуют в них – где тонко там и рвётся (слева стойка – 0, 5 Mпл; справа ригель - Mпл ), поэтому будем рисовать механизм с пластическими шарнирами в тех элементах, кторые разрушаются (хотя они все на одной прямой – на уровне ригеля). 3 Mпл α +0, 5 Mплα =Рδ =4α =10, 5/12 Mпл (сила 2Р работы не совершает, сократим на α) Р=3, 5/4 Mпл
прикладываем Mпл только к повернувшимся стержням, чтобы легче сост. Такой механизм называется балочным.
б.) Полное I, 4 шарнира. Опять шарниры в более слабых элементах. Сила Р работы не совершает.
Р=2/3 Mпл =8/12 Mпл < Ра ближе к истинному.
в.) Полное II 4 шарнира. Располагаем шарниры в более слабых стержнях
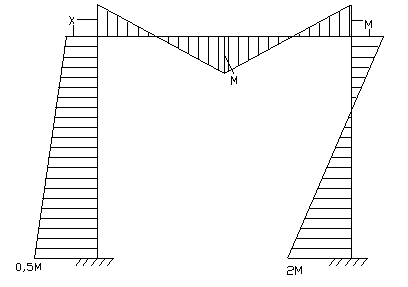
Р=6, 5/10 Mпл< Рв из трёх возможных механизмов последний даёт Рmin Рmin=0, 65 Mпл Чтобы убедиться, что это действительный механизм разрушения, для него необходимо построить предельную эпюру М, удовлетворяющую условиям равновесия. Если при этом ни в одном сечении М не привысит предельного значения – механизм истинный (по теореме о единственности решения) Откладываем сначала известные моменты в соотв. с механизмом разрушения; неизвестен лишь момент в левом верхнем узле «х», найдём его.
Для нахождения «х» можно использовать одно из трёх следующих уравнений равновесия: (остальные выполняются автоматически. т.к. в уравнения работ вошли они все). 1.)равновесие ригеля – при смещении, т.е. по перерезывающим силам:
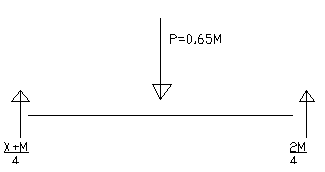
Σ Х=0 3, 9М=3, 5М-Х; Х=-0, 4 Mпл., отр – но, Х надо отложить вправо (считаем слева положит.) 2.)из равновесия силы Р:
2, 6М=Х+3М; Х=-0, 4 Mпл (тот же результат)
можно и так:
можно и так: если б не было силы Р, то и М была бы прямой и М в левом узле=3М. М=Р*4=0, 65М*4=2, 6М Т.о. получено Для данной рамы было достаточно просто установить все возможные формы (механизмы) разрушения. Нахождение Рmin не вызывало затруднений. Для более сложных рам основная трудность расчёта состоит в том, что число возможных форм их разрушения м.б. очень велико и заранее не удаётся установить все возможные формы и какая из них является действительной. Для нахождения действительной и всех возможных форм разрушения м.б. применён метод комбинированных механизмов, предложенный Саймондсом и Нилом. Согласно этому методу для любой рамы с прямолинейными стержнями (соединёнными под прямыми углами (не обязательно)) при заданной схеме загружения все возможные механизмы разрушения м.б. получены путём составления различных комбинаций относительно малого числа простых независимых механизмов (их число равно числу независимых уравнений равновесия, которое м.б. составлено для рамы, а оно в свою очередь равно m=N-Л, где N – число сечений, в которых необходимо определить момент, чтобы построить эпюру М, а Л – число лишних связей). Все простые механизмы бывают 3 – х типов6 1.) Балочный (Б) 2.) Бокового смещения (С) 3.) Узловые (У) в узлах, где больше 2х стержней соединено жёстко. Из последних (У) нельзя найти Рпред т.к. Σ М внешних сил равна нулю – он говорит лишь о равновесии узла под действием внутренних предельных моментов, действующих в пластических шарнирах, образовавшихся в стержнях, примыкающих к узлу. При комбинировании механизмов (из простых) следует рассматривать лишь такие комбинации, в которых закрывается хоть один пластический шарнир (уменьшается число внутренних моментов, входящих в уравнение работ, что может привести к уменьшению Рпред) Предельная нагрузка для комбинаций, в которых не закрылся ни один пластический шарнир получится всегда между суммарным Рпред , соответствующих для каждого из комбинированных механизмов (просто сложить оба уравнения для комбинируемых механизмов). Среди возможных рассматриваемых механизмов разрушения (простых и комбинированных) истинным будет тот, которому при заданных величинах Мпл или W пл соответствует Рmin или при заданной нагрузке Рпред соответствует Мпр max. В первую очередь следует рассматривать комбинации из простых механизмов, для которых значение Рпред является наименьшим, такие комбинации и являются истинными.
|

 или
или 


 δ =аα =вβ => β =а/вα отсюда
δ =аα =вβ => β =а/вα отсюда 
 при а=в=l/2 P=8Mпл/l, что было уже получено статическим методом. Здесь обратить внимание, что углы α и β могут быть разными при а≠ в или одинаковыми при а=в
при а=в=l/2 P=8Mпл/l, что было уже получено статическим методом. Здесь обратить внимание, что углы α и β могут быть разными при а≠ в или одинаковыми при а=в

 отсюда сократить на α
отсюда сократить на α




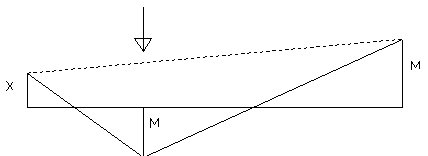
 откуда Х=-0, 4М
откуда Х=-0, 4М



