Системы с одной степенью свободы
Дифференциальное уравнение движение получим, используя статический метод.
Р(t) – приложенная нагрузка R= ry - восстанавливающая сила у - перемещение, отсчитываемое от положения статического равновесия (в котором Р= mg уравновешивается реакцией балки r – Коэффициент жесткости, численно равный силе, которую необходимо приложить к балке, чтобы сообщить статическое перемещение, равное единице. Согласно принципу Даламбера, систему можно рассматривать в состоянии равновесия, если к внешним силам добавить силы инерции.
противоположную ускорению.
где При P(t)=0 имеем свободные, или собственные колебания, которые совершает система, выведенная из положения равновесия в результате взаимодействия с каким-либо другим физическим телом после прекращения взаимодействия. Решим уравнение (1). Решение ищем в виде
1. Сила сопротивления R, или восстанавливающая сила, пропорциональна отклонению массы и всегда направлена в сторону статического равновесия. 2. Сила инерции При переходе стержня из положения равновесия в крайнее положение движение происходит замедленно и силы инерции направлены о т линии равновесия; при обратном движении последнее происходит ускоренно, поэтому силы инерции опять будут направлены в сторону от линии равновесия. Следовательно, силы инерции всегда направлены в сторону от линии статического равновесия. Характеристическое уравнение
(паре комплексно сопряженных корней соответствуют решения cos Решение уравнения y(t)= A cos Пример: определить
Лекция №20 Колебания систем с n степенями свободы. Дифференциальные уравнения движения. Рассмотрим невесомую балку с сосредоточенными массами, находящуюся под действием вынуждающей нагрузки Р(t).
Согласно принципу Даламбера систему можно рассматривать в состоянии равновесия, если к внешним силам добавить силы инерции Обозначим
С учетом (1) уравнение (2) принимает вид:
Где Система дифференциальных уравнений (3) описывает вынужденные колебания системы с n степенямисвободы. Свободные колебания. Вывод векового уравнения для определения частот собственных колебаний. Дифференциальные уравнения движения свободных колебаний получим из (3), полагая
Решение (4) представим в виде Решением уравнения Рассмотрим одно из частных решений (5)
которые подставим в (4), сократив на sin(
Система однородных линейных алгебраических уравнений (6) имеет два вида решений: 1) 2) Это возможно лишь тогда, когда определитель, составленный из коэффициентов при
Уравнение (7) впервые было получено в астрологии. Характеристические числа в нем, представляющие собой квадраты периодов движения планет, измеряются весьма большими числами- векам, поэтому данные уравнения получили название векового уравнения. Раскрывая определитель, получаем уравнение 3-ей (n-ой) степени и при его решении n значений частот. В теории колебаний доказывается, что решением (7) всегда являются только положительные числа. Совокупность всех частот называется спектром частот, первая низшая частота называется основной. Каждому значению
|


 .)
.) - сила инерции, направленная в сторону,
- сила инерции, направленная в сторону,
 ;
;  , (1)
, (1)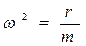 (2)
(2)


 и sin
и sin  имеет вид:
имеет вид: + B sin
+ B sin 




 .
. (1)и запишем выражение для прогиба каждой массы, который получается от действия всех сил. Ограничимся написанием одного уравнения, положив, что i=1, …n
(1)и запишем выражение для прогиба каждой массы, который получается от действия всех сил. Ограничимся написанием одного уравнения, положив, что i=1, …n (2)
(2) (3)
(3)
 , для случая n=3 (три степени свободы).
, для случая n=3 (три степени свободы). (4)
(4) - перемещение массы i от силы Р=1, приложенной к массе j, определяемые по формуле Мора.
- перемещение массы i от силы Р=1, приложенной к массе j, определяемые по формуле Мора. (5),
(5), является sin(
является sin( )
) ,
, (6)
(6) - тривиальное решение, при котором колебаний не происходит
- тривиальное решение, при котором колебаний не происходит (не все амплитуды одновременно равны нулю)
(не все амплитуды одновременно равны нулю) равен нулю. Введем обозначение
равен нулю. Введем обозначение  и запишем определитель:
и запишем определитель: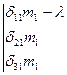

 =0 (7)
=0 (7) соответствует свой вектор
соответствует свой вектор  , то есть своя форма колебаний,
, то есть своя форма колебаний, 
 а их совокупность образует матрицу векторов: у =
а их совокупность образует матрицу векторов: у = 








