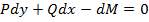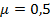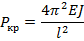Лекция № 24
Дифференциальное уравнение изгиба сжато-изогнутого стержня. Рассмотрим стержень сжатый силой Р. После потери устойчивости он деформируется. На левом конце возникают перемещения
Запишем дифференциальное уравнение изгиба стержня
Изгибающий момент в любом сечении равен
Поставим (2) в (1), введя обозначение
Решением (4) является выражение:
Постоянные интегрирования А и В найдем из граничных условий на левом конце:
подставив (6) и (7) в (5), получим выражение для прогиба в форме метода начальных параметров,
По отношению к первоначальному положению бруса
Полученные cоотношения могут быть использованы: 1) Для определения критических сил стоек постоянного сечения при различных закреплениях концов. Используя граничные условия, получим систему линейных однородных уравнений относительно начальных параметров, приравняв????? определитель, составленный из коффициентов при неизвестных, поучим уравнение устойчивости. 2) Для определения реактивных моментов и усилий по концам сжато – изогнутых стержней от смещения концов.
|

 и усилия
и усилия  .
.
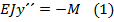

 (3)
(3) (4)
(4)


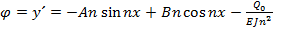 ;
; 
 получим путем последующего дифференцирования:
получим путем последующего дифференцирования: