Лекция №23
Основные расчеты стержневых систем на устойчивость. При действии на систему статически приложенных сил она может находиться в состоянии как устойчивого, так и неустойчивого равновесия. Положение системы или форма равновесия в деформированном состоянии считаются устойчивыми, если при малом отклонении от исследуемого равновесия или сколько угодно малых скоростях, сообщаемых системе (толчок), она после некоторых колебаний вернется в исходное состояние. Положение и состояние равновесия называется неустойчивым, если после малого отклонения система не возвращается в первоначальное состояние.
Устойчивостью называется способность сооружения сохранять свое первоначальноеположение или соответствующую нагрузке первоначальную форму равновесия в деформированном состоянии, то есть возвращаться в первоначальное положение после незначительного отклонения. В дальнейшем будем говорить об устойчивости формы равновесия. Переход системы из устойчивого состояния в неустойчивое называется потерей устойчивости. Границы перехода называется критическим состоянием, а соответствующая потере устойчивости нагрузка – критической. Задача расчета сооружения на устойчивость состоит в определении критических сил. Виды потери устойчивости деформированных систем. Различают потерю устойчивости I-го и II-го рода. Потеря устойчивости I-го рода характеризуется тем, что при погрузке, превышающей критическую, первоначальная форма равновесия становится неустойчивой и уступает место новой форме равновесия, качественно отличающейся от первоначальной (характер нагрузки не меняется)
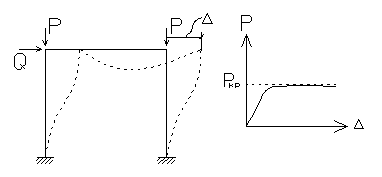
Эта потеря в Эйлеровом смысле. Потеря устойчивости I-го рода характеризуется существованием двух или нескольких форм равновесия, каждой из которых соответствует своя критическая сила. Однако наиболее вероятные является первая форма потери устойчивости. Поэтому обычно определяют наименьшую критическую нагрузку. Необходимость расчета на устойчивость заключается в следующем. Обычно приемы расчета сооружения на прочность предполагают сохранения определенного первоначального вида деформаций, соответствующей данному виду нагрузок, вплоть до момента, признаваемого опасным для прочности данного материала. Однако при нагрузке, меньше обычно допускаемой, начальная форма деформированного состояния может оказаться неустойчивой и перейти в другую форму. Новая форма создает в элементе дополнительные напряжения, не предусмотренные обычным расчетом на прочность. Может оказаться, что эти дополнительные напряжения вызовут разрушение материала элементов при нагрузках, менее допускаемых по обычному расчету на прочность для первоначальной формы равновесия. Если рассматривать потерю устойчивости равновесия в идеальной постановке, то переход одной формы в другую возможен лишь в результате какой-либо внешней причины. В реальной обстановке, кроме внешних причин, существуют и внутренние. С самого начала загружения вследствие различных несовершенств помимо основного преобладающего вида деформации неизбежны деформации и другого вида, которые в начальной стадии загружения не проявляют себя в заметной степени и не учитываются при расчете. Только с приближением нагрузки к критическому значению эти второстепенные деформации настолько искажают основную, что порождает новую форму равновесия. Для того, чтобы реализовалась потеря устойчивости I-го рода для стержневых систем должны выполняться следующие условия: а) стержни прямолинейны; б) идеальные шарниры без трения; в) сосредоточенные силы приложены по осям стержня. Хотя в природе все эти условия идеально выполняться не могут, целый ряд задач все же можно свести к рассмотрению потери устойчивости I-го рода и получить простые и достаточно точные решения. Потерей устойчивости II-го рода принято называть первое предельное состояние по несущей способности, когда при дальнейшем увеличении нагрузки равновесие между внешними и внутренними силами невозможно. Оно возможно только при уменьшении нагрузки. Потеря несущей способности трехшарнирной арки происходит без смены формы равновесия вплоть до предельной силы Рпред, при которой наступает предел возможного равновесия между внешними и внутренними силами.
При малых нагрузках влияние продольных сил на деформацию невелико, ∆ пропорционально нагрузке. С увеличением Р пропорциональность резко нарушается, деформации растут во много раз быстрее. Процесс качественно не меняется, растет лишь в количественном отношении. Нагрузка, соответствующая росту деформаций без приращения нагрузки является критической при потере устойчивости II-го типа. Расчет сооружений на потерю устойчивости I-го рода. Степень свободы в устойчивости сооружения определяется как число независимых параметров, определяющих положение системы в деформированном состоянии.
а) статический б) энергетический в) динамический
|




 Методы расчета на устойчивость.
Методы расчета на устойчивость.


