Приведение статических моментов и усилий, моментов инерции и движущихся масс к одному движению при меняющемся передаточном числе редуктора
Ряд электроприводов содержат нелинейные кинематические связи с меняющимся коэффициентом передач между двигателем и рабочим механизмом. Примером передаточного устройства с меняющимся коэффициентом передачи являются кривошипно-шатунный, кулисный и другие подобные механизмы. На рис. показана кинематическая схема электропривода с передаточным устройством в виде кривошипно-шатунного механизма (i≠ const). Радиус приведения в них является переменной величиной, зависящей от положения механизма:
Рис. 2.8 Механическая система с нелинейными кинематическими связями
Представим рассматриваемую систему в виде двухмассовой, первая масса вращается со скоростью ω и имеет момент инерции J, а вторая движется с линейной скоростью V и представляет суммарную массу m элементов, жёстко и линейно связанных с рабочим органом механизма. Рассмотрим вначале приведение статических усилий и моментов, сделав допущение о пренебрежимо малой величине потерь в кривошипном механизме, т.е. считая его к.п.д. η =1. В этом случае уравнение баланса мощности в кривошипном механизме запишется следующим образом:
где FT – тангенциальное усилие, действующее на конце кривошипа с радиусом r и полученное путем разложения и переноса исходного усилия сопротивления движению FС (рис. 2.8). Тогда момент сопротивления на валу кривошипа без учета сопротивления трения будет: Из разложения сил на рис.2.8 следует, что тогда Момент сопротивления, приведенный к валу двигателя при наличии редуктора в электроприводе с передаточным числом i:
При большой длине шатуна l, когда l/r ≥ 5 можно принять, что β ≈ 0, Таким образом, величина МСК меняется в функции углового пути кривошипного вала φ и имеет небольшую постоянную составляющую, определяемую потерями на трение в кривошипном механизме. Для приведения моментов инерции и движущихся масс к вращающемуся валу (точка «О») кривошипа составим уравнение баланса кинетической энергии кривошипного механизма в реальной и эквивалентной системах:
где Jпр.к – момент инерции кривошипного механизма, приведенный к валу кривошипа; JК.0 – момент инерции собственно кривошипа, т.е. деталей, вращающихся вокруг центра кривошипа; m – масса ползуна; VB – скорость движения ползуна. В данном выражении ввиду малости массы момента инерции шатуна составляющая запаса кинетической энергии шатуна при его вращательном и поступательном движениях не учитывается. С учетом известной зависимости V=ω ·r приведенный момент инерции кривошипного механизма будет
Это соотношение упрощается для кривошипных механизмов при β ≈ 0:
С учетом наличия в электроприводе редуктора момент инерции электропривода, приведенный к валу двигателя, имеющего собственный момент инерции JД, будет равен:
Примерный график изменения приведенного момента инерции JПР.Д=f(φ) показан на рис.2.9.
Рис.2.9 Зависимость приведенного момента от угла поворота шатуна
|

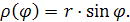

 , (2.29)
, (2.29)

 (2.30)
(2.30)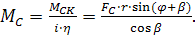 (2.31)
(2.31) и упростить выражение (2.30):
и упростить выражение (2.30): 
 (2.32)
(2.32)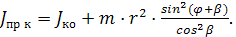 (2.33)
(2.33) (2.34)
(2.34) (2.35)
(2.35)



