Физика. Квантовая физика
ЗАДАЧА ОБ ОТНОСИТЕЛЬНОМ ДВИЖЕНИИ N ГРАВИТИРУЮЩИХ ТЕЛ
Кафедра астрономии Базей Александр Анатольевич Одесса 2001 ЗАДАЧА N ТЕЛ. Задача N тел заключается в изучении движения конечного числа материальных точек под действием их взаимного притяжения по закону Ньютона. Рассмотрим движение материальных точек вблизи центрального тела, масса которого много больше массы каждой точки. Пример такой модели – Солнечная система. Специфика Солнечной системы, в частности, в том, что {1} v в самом Солнце сосредоточено 99% массы всей системы; v планеты достаточно удалены друг от друга. Отсюда ясно, что движение каждой отдельной планеты определяется, главным образом, Солнцем. Поэтому можно говорить о взаимном движении 2-х тел, а притяжение других планет считать малым – возмущающим. Переход к системе отсчета, связанной с центром Солнца В силу сказанного, целесообразно начало системы отсчета связать с центром Солнца. Пусть имеется N гравитирующих тел: m0 x0, h0, z0; m1 x1, h1, z1; ..... mN-1 xN-1, hN-1, zN-1. Расстояние между телами - rij, В инерциальной системе отсчета уравнения движения k-го тела:
Штрих у верхнего индекса суммирования, как и ранее, означает, что в сумме опускаются слагаемые с одинаковыми индексами. Каждое слагаемое равно притяжению к каждому отдельному телу на основании закона Ньютона. Выделим притяжение Солнца:
Теперь выпишем уравнения движения Солнца:
Перейдем в уравнениях движения от сил к ускорениям. Для этого разделим систему [2] на mk, а систему [3] на m0. Полученные уравнения вычтем: [2]-[3].
Таким образом, здесь записаны дифференциальные уравнения движения относительно центра Солнца. Тем самым совершен переход к системе отсчета, связанной с центром Солнца. Сделано это путем вычитания уравнений движения Солнца из уравнений движения k–го тела. {2} Формально уравнения перехода можно записать так
Поскольку система отсчета связана с центром Солнца, его координаты равны нулю:
полное ускорение k-го ускорение k–й планеты ускорение Солнца ускорение тела Солнцем от i–х планет от i–х планет
Если в правой части в системе [4] стоят нули, (массы всех тел, за исключением m0 и mk, равны нулю) то уравнения обращаются в уравнения задачи 2-х тел. В задаче 2-х тел имеет место кеплерово движение, обычно называемое невозмущенным, а всякое отклонение от такого движения называют возмущением. {3} Системе уравнений [4] можно придать изящную форму введением некоторой функции. Надо сконструировать такую функцию, чтобы ее производные по соответствующим координатам давали правые части уравнений движения [4]. {4} Легко проверить, что такая функция
где ri – гелиоцентрические расстояния возмущающих планет с координатами (xi, yi, zi), xk, yk, zk – координаты возмущаемой планеты, rki – взаимные расстояния. Окончательно получим
Rk, наличие которого справа вызывает возмущения, называется возмущающей или пертурбационной функцией. Производные Rk по координатам точки mk дают компоненты ускорения, испытываемого телом mk в его относительном движении со стороны всех других тел, за исключением тела mk, принятого за начало координат. {5} Поскольку уравнения системы [6] являются основой теории движения планет, то их иногда называют планетной формой уравнений относительного движения. При изучении гелиоцентрического движения планет за центральное тело принимают Солнце. В этом случае возмущающая функция мала, так как в нее входят множителями планетные массы; следовательно, правые части уравнений [6] будут малы, и их влияние действительно целесообразно рассматривать как возмущения. Отсюда, в частности, трудности теории движения Луны. Система [6] порядка 6N-6 может рассматриваться как результат исключения при помощи интегралов сохранения импульса
ВОПРОСЫ. 1. В чем заключается специфика Солнечной системы с точки зрения задачи N тел? 2. Как совершить переход от инерциальной системы отсчета к системе отсчета, связанной с центром Солнца? 3. Что называют возмущением в движении тела? 4. Как строится возмущающая функция? 5. Что дают производные возмущающей функции по координатам данного тела? 6. Каков порядок системы дифференциальных уравнений, описывающих движение в задаче N тел относительно центрального тела и почему? Возмущенное движение Перепишем систему уравнений движения k-й планеты массой mk без индекса k:
где x, y, z – координаты планеты, r – расстояние этой планеты от Солнца, R - соответствующая возмущающая функция. Для Солнечной системы, как правило, полагают, что основная плоскость это плоскость эклиптики, а ось ОХ направлена в точку весны. Заметим, что система [7], описывающая возмущенное движение – система неоднородных дифференциальных уравнений, а система [8] описывающая невозмущенное движение – система однородных дифференциальных уравнений:
Эта система уже решена, проинтегрирована, и в результате получена траектория движения планеты – орбита, которая описывается кеплеровыми элементами орбиты - постоянными величинами:
Решение уравнений [7] уже не приведет к кеплерову движению по коническому сечению. Но отказываться от простого и хорошо изученного кеплерова движения нежелательно. В таком случае предпочитают считать, что планета движется по коническому сечению, но само это сечение непрерывно изменяется. Плоскость орбиты изменяется: она поворачивается и покачивается. Сама орбита как бы «дышит», вытягивается или сокращается, поворачивается в своей плоскости, оставаясь, однако, в любой момент коническим сечением. Поэтому решение уравнений [7] можно искать в той же форме, считая элементы орбиты не постоянными, а надлежащим образом выбранными функциями времени. Полученные таким образом элементы Для невозмущенного движения элементы орбиты
Для возмущенного движения элементы орбиты
Поскольку мы имеем только 3 условия [9], которым должны удовлетворять шесть функций Потребуем, чтобы не только координаты
тогда элементы Оскулирующими элементами для момента t называются такие элементы орбиты, которые дают положение и скорость для этого момента по формулам невозмущенного движения. {4}
Действительная же орбита рассматриваемой планеты, когда учтено действие возмущающих планет, отличается от эллипса, это траектория РР’. Но в точке Р в момент t0 совпадают координаты и вектор скорости планеты на возмущенной и невозмущенной орбитах. Невозмущенная орбита, имеющая общую точку и вектор скорости в момент t0 с возмущенной орбитой называется оскулирующей в момент t0, а постоянные Иными словами, оскулирующая орбита представляет собой такую орбиту, по которой бы начала двигаться в некоторый момент планета, если бы все возмущения в этот момент внезапно исчезли. Таким образом, оскулирующая орбита в момент t0 это та кеплерова орбита, которая соответствует положению и скорости рассматриваемой планеты в этот момент. Моменту t1, следующему за t0, будет соответствовать новая оскулирующая орбита с элементами Разности Возмущения в координатах определяются аналогично. Хотя оскулирующими элементами можно пользоваться при изучении любого движения, но наиболее полезен этот метод когда возмущающее ускорение мало по сравнению с притяжением центрального тела. Тогда в небольшом интервале времени можно пользоваться оскулирующей орбитой с некоторой погрешностью. Например, взяв оскулирующую орбиту для момента, лежащего в середине охватываемого наблюдениями промежутка времени, часто можно ею представить движение малой планеты или кометы в течение нескольких недель и даже месяцев с погрешностью, ничтожно малой по сравнению с ошибками наблюдений.
ВОПРОСЫ. 1. Дайте понятие мгновенных элементов орбиты. 2. Как определяется мгновенная орбита? 3. В чем отличие мгновенных и оскулирующих элементов орбиты? 4. Что называется оскулирующими элементами орбиты? 5. Что называется оскулирующей орбитой? Отличается ли скорость планеты на оскулирующей и на мгновенной орбите в момент оскуляции? Отличается ли скорость планеты на истинной и на мгновенной орбите в момент оскуляции?
Уравнения Лагранжа Далее будем искать вариацию оскулирующей орбиты. Перепишем систему уравнений [11] несколько иначе:
где
Такое разделение элементов орбиты можно заметить, например, в задаче 2-х тел при вычислении координат:
В возмущенном движении
ускорение в ускорение в возмущенном невозмущенном движении движении
Сравнивая полученное уравнение с системой [7], приходим к выводу
Теперь продифференцируем систему [12] по времени:
Но
В системы [14] и [15] входят вариации элементов орбиты
Для решения уравнений систем [14] и [15] относительно Производные возмущающей функции по координатам Домножим [14]
Под знаками сумм записаны скобки Пуассона:
Аналогично -
Сложим эти три уравнения
Введем обозначение
Выражения вида Вспомним, что возмущающая функция R зависит от координат x, y, z рассматриваемой планеты и xk, yk, zk возмущающих планет или, что то же самое, R зависит от их элементов орбиты
Итак,
Здесь записано 3 уравнения (i=1, 2, 3). Аналогичные уравнения для элементов орбиты группы
Системы [18] и [19] – уравнения Лагранжа для вариации элементов орбиты Если
Надо отметить, что в общем случае производные элементов орбиты
ВОПРОСЫ. 1. Отличается ли скорость планеты на оскулирующей и на истинной орбите в момент оскуляции? 2. Что называется скобками Лагранжа? 3. В чем смысл уравнений Лагранжа? Свойства скобок Лагранжа В этом пункте под элементом орбиты
Свойство I. Свойство II. Свойство III. Элементы орбиты характеризуют движение по коническому сечению. Движение по произвольной траектории в общем случае нельзя описывать с помощью кеплеровых элементов орбиты. В данном случае описание произвольного движения производится с помощью медленно изменяющихся кеплеровых элементов орбиты (поскольку произвольная траектория незначительно отличается от конического сечения из-за малости возмущающих сил). Для доказательства этого свойства необходимо воспользоваться уравнениями невозмущенного движения [8]. Тогда координаты x, y, z из [8] однозначно выражаются через кеплеровы элементы орбиты.
Введем обозначение
Продифференцируем скобку Пуассона по времени:
Получим
А так как скобка Лагранжа это сумма трех скобок Пуассона, то складывая
что и требовалось доказать. Явная независимость скобок Лагранжа от времени позволяет после их вычисления придать времени произвольное значение. Это свойство широко используется.
ВОПРОСЫ. 1. Назовите свойства скобок Лагранжа? Вычисление скобок Лагранжа Для вычисления скобок Лагранжа потребуется вычислить частные производные координат по элементам орбиты.
Из сферической геометрии известно
Величины дуг
тогда из сферического треугольника CNХ, где
Из сферического треугольника CNY, где
Дуга CZ соединяет полюсы больших кругов – эклиптики и орбиты, угол между которыми i
Итак, направляющие косинусы всех трех осей орбитальной системы отсчета относительно эклиптической
Производные направляющих косинусов по элементам орбиты
ВЫЧИСЛЕНИЕ СКОБОК ЛАГРАНЖА ТИПА По определению
Здесь координаты
Теперь
раскрываем скобки и приводим подобные слагаемые
Сомножитель при сумме – постоянная величина (закон сохранения момента импульса, «ЗАДАЧА 2-х ТЕЛ» - [37]):
( Итак
Для дальнейших вычислений найдем некоторые вспомогательные величины. Пусть g - любой из 6-ти элементов орбиты. Поскольку
Пользуясь этими равенствами, вычислим
Легко проверить, что
Продифференцируем равенство [23] по d, где d – тоже любой из 6-ти элементов орбиты:
Перепишем [23]
Вычтем [25]-[24]:
Теперь вернемся к формуле [21], с учетом полученного:
В частности, если
Если
В правой части перейдем к другим элементам орбиты:
Похожим образом вычисляются скобки Лагранжа типа
Здесь
Таким образом, все шесть уравнений Лагранжа [18] и [19] в развернутом виде:
Подставляя сюда значения скобок Лагранжа:
Систему уравнений Лагранжа [28] надо решить относительно
Отметим, что время входит в уравнения Лагранжа только посредством производных пертурбационных функций R. {1} Чтобы фактически выполнить интегрирование, надо пертурбационные функции представить в виде явных функций времени. Это возможно, лишь прибегнув к разложению их в бесконечные ряды. При изучении Солнечной системы часто встречаются движения по слабонаклоненным орбитам. Чем ближе к нулю наклонение i, тем менее определенным становится положение восходящего узла орбиты. При i=0 положение узла становится полностью неопределенным. Вследствие этого долгота восходящего узла W находится из наблюдений с ошибкой, неограниченно возрастающей по мере приближения i к нулю. Чтобы избежать возникающих отсюда неудобств при определении положения перигелия, вместо аргумента перигелия w пользуются элементом орбиты
ВОПРОСЫ. 1. Входит ли в уравнения Лагранжа время? 2. Что называется долготой перигелия и с какой целью она вводится?
Уравнения Лагранжа были широко использованы для аналитического изучения движений в Солнечной системе. Решение системы [29] можно искать методом последовательных приближений из-за малости планетных масс по сравнению с солнечной. Тогда решение будет иметь вид
Ряды расположены по целым степеням масс, через a0, e0,... обозначены оскулирующие элементы орбиты в некоторый начальный момент времени t=0. Через Для оценки важности отдельных возмущений употребляется несколько характеристик. Прежде всего – это порядок возмущения. Чем ниже порядок, тем больше (при прочих равных условиях) влияние рассматриваемого возмущения. {2} С другой стороны все слагаемые в решениях типа [30] делятся на периодические, вековые и смешанные возмущения. Кроме того, возмущения характеризуются своей степенью, рангом и классом. Эти характеристики мы здесь не рассматриваем. При изучении движения планет приходится иметь дело главным образом с периодическими возмущениями 1-го порядка. В зависимости от величины периода, возмущения делятся на: v короткопериодические – их периоды меньше или равны периодам возмущающей или возмущаемой планет, амплитуды таких членов и соответствующие возмущения обычно невелики; {3} v долгопериодические – их наличие часто обусловлено приблизительной соизмеримостью средних угловых движений n возмущающей и возмущаемой планет, величины их обычно на 2 порядка больше величин короткопериодических членов, и поэтому им соответствуют очень большие возмущения. {4} С долгопериодическими возмущениями астрономы впервые встретились при попытке объяснить движения Юпитера и Сатурна их взаимным притяжением. Под влиянием долгопериодических неравенств долгота Сатурна может изменяться на 50’. При далеких сближениях с планетами обычно преобладают долгопериодические возмущения, при тесных сближениях возникает «удар» – преобладают короткопериодические возмущения с большими амплитудами. Наличие вековых членов первого порядка обусловлено той частью возмущающей функции, которая при разложении в ряд не зависит от времени. Если при решении уравнений Лагранжа возникают вековые члены в возмущении данного элемента орбиты, то он будет монотонно изменяться с малой постоянной скоростью (вековым образом) без ограничений. {5} Теорема Лапласа-Лагранжа. Если средние движения n планет несоизмеримы, то большие полуоси а не имеют вековых возмущений 1-го порядка. {6} Эта теорема связана с вопросом об устойчивости Солнечной системы. При рассмотрении возмущений 2-го и более высоких порядков в изменении большой полуоси а появляются вековые члены, и следовательно, область изменения а уже не будет ограниченной для всех значений времени – устойчивость, в прежнем смысле, будет отсутствовать. На первый взгляд кажется, что об устойчивости Солнечной системы говорить нельзя. Но здесь надо вспомнить, что при решении уравнений Лагранжа возмущающая функция R раскладывается в ряд, а значит промежуток времени, на котором это разложение справедливо – ограничен. Поэтому ясно, что возмущения высоких порядков получены с определенной точностью для ограниченных интервалов времени. Таким образом, об устойчивости Солнечной системы этот анализ ничего не говорит. {7} С другой стороны, есть основания полагать, что вековые возмущения это периодические возмущения с очень большими периодами -продолжительностью несколько тысяч лет. Вековой член lt может оказаться приближением к долгопериодическому члену sin lt, когда lt мало. Это справедливо для любого элемента орбиты.
ВОПРОСЫ. 1. Что называется возмущениями n–го порядка? 2. Что больше при прочих равных условиях: влияние возмущения 1-го или 2-го порядка? 3. Дайте понятие короткопериодических возмущений. 4. Дайте понятие долгопериодических возмущений, когда они обычно возникают? 5. Дайте понятие вековых возмущений. 6. Сформулируйте теорему Лапласа-Лагранжа. 7. Известно, что при рассмотрении возмущений 2-го и высших порядков появляются вековые возмущения больших полуосей орбит планет. Что можно сказать об устойчивости Солнечной системы?
ВОЗМУЩЕНИЯ. ГЕОМЕТРИЧЕСКИЕ СООБРАЖЕНИЯ. Возмущающая сила Напомним, что кеплерово движение в задаче 2-х тел, обычно называют невозмущенным, а всякое отклонение от такого движения называют возмущением. Предположим, что тело m движется из точки P0 в направлении Q0 со скоростью V0 и что кроме притяжения тела S не имеется сил, действующих на него. Тогда согласно результатам задачи 2-х тел оно будет двигаться по коническому сечению С0, элементы которого однозначно определены начальными условиями. Предположим, что когда m приходит в точку P1, то оно подвергается мгновенному импульсу в направлении P1Q1; это положение и новый вектор скорости определяют новое коническое сечение С1, по которому будет дви
|

 .
. [1]
[1] [2]
[2] [3]
[3]

 . Уравнения движения в неинерциальной системе отсчета поэтому
. Уравнения движения в неинерциальной системе отсчета поэтому [4]
[4] [4]
[4] , [5]
, [5] [6]
[6]
 (формулы [3] и [4] из главы “ЗАДАЧА О ДВИЖЕНИИ N ГРАВИТИРУЮЩИХ ТЕЛ” (введение)) из системы [1] порядка 6N шести величин
(формулы [3] и [4] из главы “ЗАДАЧА О ДВИЖЕНИИ N ГРАВИТИРУЮЩИХ ТЕЛ” (введение)) из системы [1] порядка 6N шести величин  . {6}
. {6} [7]
[7] ,
, [8]
[8] [9]
[9] называются мгновенными элементами орбиты. {1} Совокупность этих элементов дает мгновенную орбиту планеты для момента t. {2} Знание мгновенной орбиты позволяет вычислять координаты планеты для любого момента t по формулам кеплерова движения [9].
называются мгновенными элементами орбиты. {1} Совокупность этих элементов дает мгновенную орбиту планеты для момента t. {2} Знание мгновенной орбиты позволяет вычислять координаты планеты для любого момента t по формулам кеплерова движения [9]. постоянны. Поэтому
постоянны. Поэтому ,
,  ,
,  .
. ,
, ,
,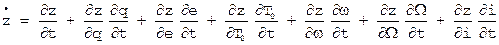 .
. , но и их производные
, но и их производные  выражались через мгновенные элементы орбиты. {3} То есть требуем
выражались через мгновенные элементы орбиты. {3} То есть требуем ,
,  ,
,  , или
, или ,
,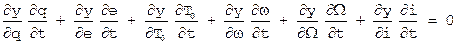 , [10]
, [10] ,
, Пусть Р – положение планеты в момент t0. Если в этот момент возмущающие планеты прекращают свое действие на тело Р, то его орбита будет эллипсом PQ с постоянными элементами
Пусть Р – положение планеты в момент t0. Если в этот момент возмущающие планеты прекращают свое действие на тело Р, то его орбита будет эллипсом PQ с постоянными элементами  [11]
[11] - оскулирующими элементами орбиты для момента t0. {5} («оскулировать» - значит соприкасаться)
- оскулирующими элементами орбиты для момента t0. {5} («оскулировать» - значит соприкасаться) , связанными с новыми координатами и скоростью планеты в ее действительном движении. И так далее, - оскулирующая орбита может быть вычислена для любого момента времени, каково бы ни было движение планеты, если известны ее положение и скорость в этот момент времени.
, связанными с новыми координатами и скоростью планеты в ее действительном движении. И так далее, - оскулирующая орбита может быть вычислена для любого момента времени, каково бы ни было движение планеты, если известны ее положение и скорость в этот момент времени. называются возмущениями в элементах орбиты за время t1-t0.
называются возмущениями в элементах орбиты за время t1-t0. [12]
[12] [13]
[13] - сопряженные элементы орбиты:
- сопряженные элементы орбиты: ,
,  - среднее суточное движение,
- среднее суточное движение, .
. .
.

 ,
,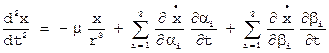 ,
, .
.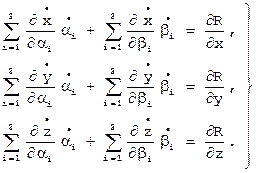 [14]
[14]
 , поскольку по определению, движение по оскулирующей орбите происходит с той же скоростью, что и по истинной траектории в момент оскуляции. {1} Поэтому
, поскольку по определению, движение по оскулирующей орбите происходит с той же скоростью, что и по истинной траектории в момент оскуляции. {1} Поэтому [15]
[15] . В совокупности имеем 6 уравнений и 6 неизвестных вариаций
. В совокупности имеем 6 уравнений и 6 неизвестных вариаций  заменим на производные по элементам орбиты
заменим на производные по элементам орбиты  . Будем проводить преобразования первых уравнений систем [14] и [15]. Действия с другими уравнениями аналогичны.
. Будем проводить преобразования первых уравнений систем [14] и [15]. Действия с другими уравнениями аналогичны. ; [15]
; [15]  и вычтем из первого произведения второе.
и вычтем из первого произведения второе. ,
, ,
, .
.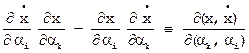 ,
,  , тогда
, тогда . [16]
. [16] ,
, .
.

 [17]
[17] , определяемые равенством [17], называются скобками Лагранжа относительно
, определяемые равенством [17], называются скобками Лагранжа относительно  . Следовательно
. Следовательно .
. . [18]
. [18] . [19]
. [19] . Если известны значения скобок Лагранжа и производные возмущающей функции по соответствующим элементам орбиты, то легко можно найти вариации элементов орбиты.
. Если известны значения скобок Лагранжа и производные возмущающей функции по соответствующим элементам орбиты, то легко можно найти вариации элементов орбиты. - оскулирующие элементы орбиты известны на какую-либо эпоху t, то в эпоху t+Dt элементы орбиты:
- оскулирующие элементы орбиты известны на какую-либо эпоху t, то в эпоху t+Dt элементы орбиты: ,
, - в этом смысл уравнений Лагранжа. {3}
- в этом смысл уравнений Лагранжа. {3}
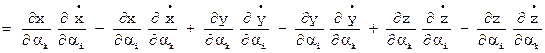 .
. - это очевидно из определения.
- это очевидно из определения. - это следует из определения скобок Пуассона.
- это следует из определения скобок Пуассона. - скобки Лагранжа явно от времени не зависят. {1} Докажем это свойство.
- скобки Лагранжа явно от времени не зависят. {1} Докажем это свойство.
 . Тогда эти уравнения примут вид
. Тогда эти уравнения примут вид .
.
 , где
, где  . Подставим эту производную
. Подставим эту производную , и прибавим ноль.
, и прибавим ноль.

 .
. ,
, Пусть x, y, z – эклиптические координаты возмущаемой планеты. Положение плоскости оскулирующей орбиты и направление на перигелий относительно эклиптической системы отсчета определяется элементами
Пусть x, y, z – эклиптические координаты возмущаемой планеты. Положение плоскости оскулирующей орбиты и направление на перигелий относительно эклиптической системы отсчета определяется элементами  . Введем орбитальные прямоугольные координаты планеты
. Введем орбитальные прямоугольные координаты планеты 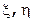 . Ось
. Ось  направлена на перигелий орбиты, ось
направлена на перигелий орбиты, ось 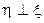 . Направляющие косинусы этих осей относительно эклиптической системы отсчета x, y, z были получены в главе «ЗАДАЧА 2-х ТЕЛ» и определены там равенствами [39]. Там же они обозначены как px, py, pz, qx, qy, qz. Найдем теперь направляющие косинусы прямой, направленной на полюс орбиты С.
. Направляющие косинусы этих осей относительно эклиптической системы отсчета x, y, z были получены в главе «ЗАДАЧА 2-х ТЕЛ» и определены там равенствами [39]. Там же они обозначены как px, py, pz, qx, qy, qz. Найдем теперь направляющие косинусы прямой, направленной на полюс орбиты С.

 ,
, ,
,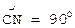 ,
, следует
следует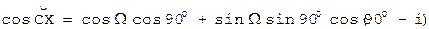 или
или .
. ,
, 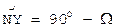
 или
или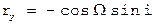 .
. или
или

 [20]
[20]
 легко вычисляются
легко вычисляются
 .
. зависят от элементов орбиты
зависят от элементов орбиты  не зависят от
не зависят от  ).
).
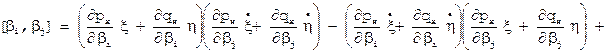








 , где
, где  .
. , поскольку слева стоят орбитальные координаты)
, поскольку слева стоят орбитальные координаты) [21]
[21]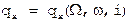 , то
, то  , и, подставляя производные из таблицы
, и, подставляя производные из таблицы аналогично
аналогично [22]
[22]
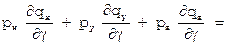

 .
. , и по свойству направляющих косинусов
, и по свойству направляющих косинусов  .
.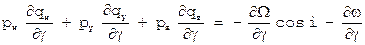 [23]
[23] [24]
[24] и снова продифференцируем по g:
и снова продифференцируем по g: [25]
[25]
 [26]
[26] [27]
[27] , то
, то ,
, .
. , то
, то .
. , где n - среднее движение («ЗАДАЧА 2-х ТЕЛ» - [59]:
, где n - среднее движение («ЗАДАЧА 2-х ТЕЛ» - [59]:  ),
),
 и
и  . Значения всех скобок Лагранжа приведены в следующей таблице (первым в скобках Лагранжа выбирается элемент, стоящий в заголовке строки, вторым – стоящий в заголовке столбца):
. Значения всех скобок Лагранжа приведены в следующей таблице (первым в скобках Лагранжа выбирается элемент, стоящий в заголовке строки, вторым – стоящий в заголовке столбца):









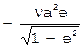

 .
. ,
, ,
, ,
,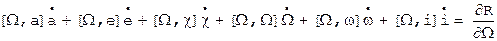 ,
, ,
, .
. ,
, ,
, , [28]
, [28] ,
, ,
, .
. :
: ,
, ,
, , [29]
, [29] ,
, ,
, .
. , называемым долготой перигелия. {2} Кроме того, Вместо элемента
, называемым долготой перигелия. {2} Кроме того, Вместо элемента  вводят среднюю долготу в эпоху
вводят среднюю долготу в эпоху  . Тогда уравнения Лагранжа выглядят немного иначе.
. Тогда уравнения Лагранжа выглядят немного иначе. Возмущенное движение в Солнечной системе
Возмущенное движение в Солнечной системе ,
, , [30]
, [30]
 обозначены члены рядов n-й степени относительно масс. Эти величины называются возмущениями n-го порядка. {1}
обозначены члены рядов n-й степени относительно масс. Эти величины называются возмущениями n-го порядка. {1}


