59. Рассмотрим эрмитов оператор 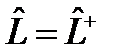 , имеющий дискретный спектр (п. 56). Среди всех возможных его собственных функций y m выберем такие функции, норма которых равна 1, т.е.
, имеющий дискретный спектр (п. 56). Среди всех возможных его собственных функций y m выберем такие функции, норма которых равна 1, т.е.
 . (55)
. (55)
Условие (55) называется условием нормировки волновой функции (вектора состояния). В соответствии со результатами, полученным в пп. 51, 55, среди всех функций y m можно выбрать такие, что при различных m и n функции y m и y n (вектора состояния  и
и  ) ортогональны друг к другу. Вместе с условием нормировки (55) требование ортогональности функций y m и y n (векторов состояния
) ортогональны друг к другу. Вместе с условием нормировки (55) требование ортогональности функций y m и y n (векторов состояния  и
и  ) может быть записано в виде
) может быть записано в виде
 , (56)
, (56)
где d mn – символы Кронекера.
В функциональном анализе доказывается, что собственные функции эрмитового оператора образуют базис в пространстве функций, на котором он определен. В случае дискретного спектра это означает, что любую скалярную функцию f (q) из области определения эрмитового оператора 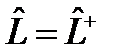 с дискретным спектром можно разложить в функциональный ряд по собственным функциям y n оператора
с дискретным спектром можно разложить в функциональный ряд по собственным функциям y n оператора  :
:
 , (57)
, (57)
где коэффициенты разложения fn однозначно определены и в силу (56) могут быть вычислены по правилу
 (58)
(58)
(выведите формулу (58), скалярно умножая обе части (57) на одну из собственных функций оператора  и принимая во внимание условие ортонормировки (56)). Набор чисел (58) полностью определяет состояние, описываемое функцией f (q).
и принимая во внимание условие ортонормировки (56)). Набор чисел (58) полностью определяет состояние, описываемое функцией f (q).
60. Подстановка (58) в (57):
 ,
,
позволяет сделать вывод, что
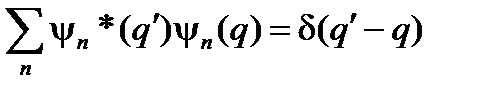 , (59)
, (59)
где многомерная дельта-функция d(q ¢ – q) определена в (13). Условие (59) можно рассматривать как некоторую модель дельта-функции. Она строится, как видно из (59), по полной системе собственных функций некоторого эрмитового оператора.
61. Пусть функции y n являются собственными функциями некоторого эрмитового интегрального оператора  , т.е. оператора, действующего на функции по правилу (11), ядро которого L (q, q ¢) обладает свойством (40). Можно показать, что функция L (q, q ¢) представима в виде
, т.е. оператора, действующего на функции по правилу (11), ядро которого L (q, q ¢) обладает свойством (40). Можно показать, что функция L (q, q ¢) представима в виде
 , (60)
, (60)
где l n – собственные числа оператора  (покажите это, воспользовавшись (11) для записи явного вида левой части (54) и представлением дельта-функции (59)).
(покажите это, воспользовавшись (11) для записи явного вида левой части (54) и представлением дельта-функции (59)).
62. Перепишем соотношения (57), (58) на языке соответствующих векторов состояния:
 , (57¢)
, (57¢)
 . (58¢)
. (58¢)
Говорят, что коэффициенты fn представляют состояние 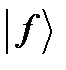 в базисе собственных векторов эрмитового оператора
в базисе собственных векторов эрмитового оператора  . Сумма в (57¢), вообще говоря, бесконечна, и поэтому требует более строгого определения. Именно, записи (57¢), (58¢) непротиворечивы, если для любого вектора состояния
. Сумма в (57¢), вообще говоря, бесконечна, и поэтому требует более строгого определения. Именно, записи (57¢), (58¢) непротиворечивы, если для любого вектора состояния  числовой ряд
числовой ряд
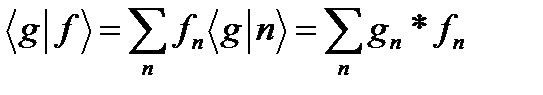
абсолютно сходится.
Подстановка (58¢) в (57¢) дает:
 ,
,
откуда следует, что
 . (61)
. (61)
Это условие является эквивалентом условия (59), так как дельта-функция является ядром интегрального представления единичного оператора  .
.
В левой части (61) стоит сумма т.н. прямых, или диадных произведений кэт-векторов на бра-векторы, которые рассматриваются как операторы. Каждый из них в отдельности является проективным оператором. Действительно, возводя оператор  в квадрат, в силу условия нормировки (55) получим:
в квадрат, в силу условия нормировки (55) получим:
 ,
,
что соответствует определению проективного оператора (24). Оператор  производит ортогональную проекцию состояния
производит ортогональную проекцию состояния 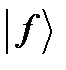 на состояние
на состояние  . Величина этой проекции равна fn и определяется по формуле (58¢).
. Величина этой проекции равна fn и определяется по формуле (58¢).
Благодаря условиям ортогональности (56) любая конечная и даже бесконечная частичная сумма  также будет проективным оператором (проверьте!).
также будет проективным оператором (проверьте!).
63. Рассмотрим разложение образа  функции f (q), полученное с помощью некоторого линейного оператора
функции f (q), полученное с помощью некоторого линейного оператора  , по собственным функциям y m оператора
, по собственным функциям y m оператора  :
:
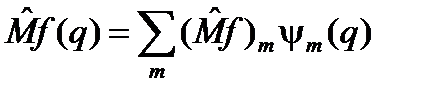 , (62.1)
, (62.1)
где  – соответствующие коэффициенты разложения. С другой стороны, действуя линейным оператором
– соответствующие коэффициенты разложения. С другой стороны, действуя линейным оператором  на разложение (57), найдем, что
на разложение (57), найдем, что
 . (62.2)
. (62.2)
Запишем разложение функций  по собственным функциям y m оператора
по собственным функциям y m оператора  в виде
в виде
 (62.3)
(62.3)
и подставим (62.3) в (62.2), а затем сравним полученный результат с (62.1). В итоге найдем, что
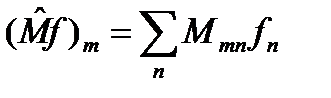 , (63)
, (63)
где, согласно (62.3) и свойству (56) ортонормированности функций y m
 (64)
(64)
– матричные элементы оператора  относительно собственных функций y m и y n эрмитового оператора
относительно собственных функций y m и y n эрмитового оператора  , общее определение которых дано в (43). В этом случае величины (64) будем называть матричными элементами оператора
, общее определение которых дано в (43). В этом случае величины (64) будем называть матричными элементами оператора  в базисе
в базисе  собственных векторов состояния эрмитового оператора
собственных векторов состояния эрмитового оператора  .
.
64. Запишем (62.1) в обозначениях Дирака
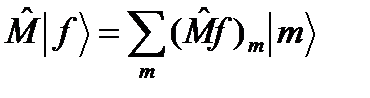
и подставим сюда представление (63), заменив fn на дираковскую скобку  согласно (58¢). В результате будем иметь:
согласно (58¢). В результате будем иметь:
 .
.
Отсюда видно, что оператор  , как оператор, действующий в пространстве векторов состояния, можно представить через его матричные элементы в базисе
, как оператор, действующий в пространстве векторов состояния, можно представить через его матричные элементы в базисе  следующим образом:
следующим образом:
 . (65)
. (65)
Говорят, что матрица (Mmn), составленная из матричных элементов оператора  в базисе собственных векторов состояния эрмитового оператора
в базисе собственных векторов состояния эрмитового оператора  , представляет оператор
, представляет оператор  в этом базисе. Выражение, стоящее в правой части (65) есть прямая запись оператора
в этом базисе. Выражение, стоящее в правой части (65) есть прямая запись оператора  в базисе, составленном из собственных векторов эрмитового оператора
в базисе, составленном из собственных векторов эрмитового оператора  . В частности, если Mmn = d mn, то (65) дает представление единичного оператора (61).
. В частности, если Mmn = d mn, то (65) дает представление единичного оператора (61).
Если оператор  эрмитов, то и представляющая его в базисе собственных векторов эрмитового оператора
эрмитов, то и представляющая его в базисе собственных векторов эрмитового оператора  матрица (Mmn) тоже будет эрмитовой:
матрица (Mmn) тоже будет эрмитовой:
Mnm * = Mmn,
т.е. диагональные матричные элементы эрмитового оператора вещественны, а недиагональные элементы, стоящие в противоположных местах матрицы относительно ее диагонали, являются комплексно сопряженными числами.
Если оператор симметричен (антисимметричен), то представляющая его матрица будет тоже симметрична (антисимметрична). Перечень подобных утверждений можно продолжить, рассматривая матричные элементы унитарных, проективных и других операторов.
65. В частном случае, когда оператор  совпадает с оператором
совпадает с оператором  , как видно из (64) и условия ортонормировки (56), матрица (Lmn), представляющая этот оператор в базисе собственных векторов, будет диагональна:
, как видно из (64) и условия ортонормировки (56), матрица (Lmn), представляющая этот оператор в базисе собственных векторов, будет диагональна:
Lmn = l n d mn, (66)
где l n – собственные значения оператора  . Согласно (65) оператор
. Согласно (65) оператор  , действующий в пространстве векторов состояния, можно представить в собственном базисе следующим образом:
, действующий в пространстве векторов состояния, можно представить в собственном базисе следующим образом:
 . (66¢)
. (66¢)
66. Говорят, что числа fn, определенные по формуле (58), или (58¢), задают волновую функцию f (q), или соответствующий вектор состояния  в представлении, связанном с оператором
в представлении, связанном с оператором  , или в L-представлении. Числа Mmn задают оператор
, или в L-представлении. Числа Mmn задают оператор  в L-представлении.
в L-представлении.
Таким образом, представление в квантовой механике можно считать аналогом системы декартовых координат в классической механике.
67. Рассмотрим наряду с эрмитовым оператором  , имеющем дискретный спектр собственных значений l n, эрмитов оператор
, имеющем дискретный спектр собственных значений l n, эрмитов оператор  , действующий на множестве тех же состояний, на которых действует оператор
, действующий на множестве тех же состояний, на которых действует оператор  . Пусть спектр собственных значений k n ¢ оператора
. Пусть спектр собственных значений k n ¢ оператора  будет также дискретен и его мощность будет равна мощности спектра оператора
будет также дискретен и его мощность будет равна мощности спектра оператора  . Тогда собственные векторы
. Тогда собственные векторы  оператора
оператора  можно разложить по собственным векторам
можно разложить по собственным векторам  оператора
оператора  и наоборот:
и наоборот:
 , (67)
, (67)
где  и
и  – соответствующие коэффициенты разложения, которые связывают упорядоченные совокупности собственных функций (векторов) этих операторов и их совокупность играет роль связывающей величины при преобразованиях базиса в пространстве волновых функций (векторов состояния). Из условия ортонормированности каждой систем векторов
– соответствующие коэффициенты разложения, которые связывают упорядоченные совокупности собственных функций (векторов) этих операторов и их совокупность играет роль связывающей величины при преобразованиях базиса в пространстве волновых функций (векторов состояния). Из условия ортонормированности каждой систем векторов  и
и  в отдельности следует, что
в отдельности следует, что
 ,
,
т.е. матрицы коэффициентов разложения  и
и  являются унитарными. Матрица
являются унитарными. Матрица  является обратной по отношению к
является обратной по отношению к  , а, следовательно, эрмитовски сопряжена к ней:
, а, следовательно, эрмитовски сопряжена к ней:  . Следовательно, оператор
. Следовательно, оператор  связан с оператором
связан с оператором  унитарным преобразованием
унитарным преобразованием
 ,
,
матричные элементы которого относительно векторов  и
и  равны коэффициентам разложения в (67):
равны коэффициентам разложения в (67):  . В силу единственности разложения (67) унитарный оператор
. В силу единственности разложения (67) унитарный оператор  в заданных базисах определен однозначным образом. Как было отмечено в п. 60, множества собственных значений операторов
в заданных базисах определен однозначным образом. Как было отмечено в п. 60, множества собственных значений операторов  и
и  совпадают. Поэтому собственные k n ¢ значения оператора
совпадают. Поэтому собственные k n ¢ значения оператора  можно рассматривать как особые линейные комбинации собственных значений l т оператора
можно рассматривать как особые линейные комбинации собственных значений l т оператора  , в которых происходит перемешивание их номеров.
, в которых происходит перемешивание их номеров.
Упражнение. Покажите, что
 .
.
68. Волновую функцию f (q) часто называют волновой функцией в координатном представлении. Аналогично, оператор производной по обобщенным координатам ¶ i тоже относят к координатном представлению. Однако, в этом случае слово «представление» используется в ином смысле, нежели в рассмотренном выше случае, когда говорится о представлении, связанном с оператором  .
.

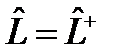 , имеющий дискретный спектр (п. 56). Среди всех возможных его собственных функций y m выберем такие функции, норма которых равна 1, т.е.
, имеющий дискретный спектр (п. 56). Среди всех возможных его собственных функций y m выберем такие функции, норма которых равна 1, т.е. . (55)
. (55) и
и  ) ортогональны друг к другу. Вместе с условием нормировки (55) требование ортогональности функций y m и y n (векторов состояния
) ортогональны друг к другу. Вместе с условием нормировки (55) требование ортогональности функций y m и y n (векторов состояния  , (56)
, (56) :
: , (57)
, (57) (58)
(58) ,
,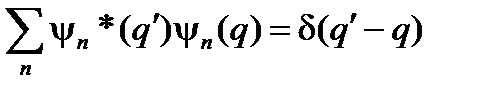 , (59)
, (59) , (60)
, (60) , (57¢)
, (57¢) . (58¢)
. (58¢)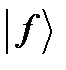 в базисе собственных векторов эрмитового оператора
в базисе собственных векторов эрмитового оператора  числовой ряд
числовой ряд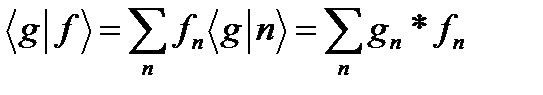
 ,
, . (61)
. (61) .
. в квадрат, в силу условия нормировки (55) получим:
в квадрат, в силу условия нормировки (55) получим: ,
, . Величина этой проекции равна fn и определяется по формуле (58¢).
. Величина этой проекции равна fn и определяется по формуле (58¢). также будет проективным оператором (проверьте!).
также будет проективным оператором (проверьте!). функции f (q), полученное с помощью некоторого линейного оператора
функции f (q), полученное с помощью некоторого линейного оператора  , по собственным функциям y m оператора
, по собственным функциям y m оператора 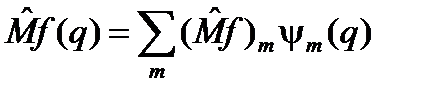 , (62.1)
, (62.1) – соответствующие коэффициенты разложения. С другой стороны, действуя линейным оператором
– соответствующие коэффициенты разложения. С другой стороны, действуя линейным оператором  . (62.2)
. (62.2) по собственным функциям y m оператора
по собственным функциям y m оператора  (62.3)
(62.3)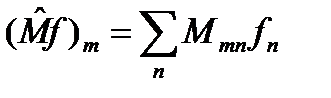 , (63)
, (63) (64)
(64) собственных векторов состояния эрмитового оператора
собственных векторов состояния эрмитового оператора 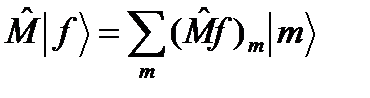
 согласно (58¢). В результате будем иметь:
согласно (58¢). В результате будем иметь: .
. . (65)
. (65) . (66¢)
. (66¢) в представлении, связанном с оператором
в представлении, связанном с оператором  , действующий на множестве тех же состояний, на которых действует оператор
, действующий на множестве тех же состояний, на которых действует оператор  оператора
оператора  оператора
оператора  , (67)
, (67) и
и  – соответствующие коэффициенты разложения, которые связывают упорядоченные совокупности собственных функций (векторов) этих операторов и их совокупность играет роль связывающей величины при преобразованиях базиса в пространстве волновых функций (векторов состояния). Из условия ортонормированности каждой систем векторов
– соответствующие коэффициенты разложения, которые связывают упорядоченные совокупности собственных функций (векторов) этих операторов и их совокупность играет роль связывающей величины при преобразованиях базиса в пространстве волновых функций (векторов состояния). Из условия ортонормированности каждой систем векторов  в отдельности следует, что
в отдельности следует, что ,
, является обратной по отношению к
является обратной по отношению к  . Следовательно, оператор
. Следовательно, оператор  ,
, и
и  равны коэффициентам разложения в (67):
равны коэффициентам разложения в (67):  . В силу единственности разложения (67) унитарный оператор
. В силу единственности разложения (67) унитарный оператор  в заданных базисах определен однозначным образом. Как было отмечено в п. 60, множества собственных значений операторов
в заданных базисах определен однозначным образом. Как было отмечено в п. 60, множества собственных значений операторов  .
.


