Пространство волновых функций
1. Объектом изучения в квантовой механике являются механические системы, положение которых в пространстве характеризуется обобщенными координатами qi, i = 1, …, s, где s – число степеней свободы. 2. Будем рассматривать случаи, когда состояние квантовомеханической системы можно описать с помощью комплекснозначных функций обобщенных координат qi: y(q) = y(q 1, …, qs), являющихся элементами линейного пространства A над полем комплексных чисел C. На эти функции накладываются требования дифференцируемости необходимое число раз и квадратичной интегрируемости. В квантовой механике эти функции называются волновыми функциями. 3. На пространстве волновых функций определяется скалярное произведение функций
где dsq = dq 1… dqs – элемент координатного объема в конфигурационном пространстве механической системы. В частности скалярный квадрат функции
что объясняет необходимость наложения на волновые функции условия квадратичной интегрируемости. Из (1) вытекает следующее свойство скалярного произведения
4. С помощью скалярного произведения (1) вводится понятие нормы вектора y(q), или его длины:
так как интеграл Легко видеть, что (2) действительно обладает всеми свойствами нормы:
5. Пространство A может быть конечномерным или бесконечномерным. В последнем случае число измерений может быть как счетно, так и несчетно. Такое пространство со скалярным произведением (1) называется гильбертовым пространством. 6. Наряду с пространством A волновых функций y(q), заданных в некоторой области конфигурационного пространства механической системы можно рассматривать пространство Acket абстрактных векторов
Векторы Число 7. Волновая функция y(q) может представлять собой набор волновых функций col(y1(q), …, y N (q)) – координат некоторого вектора в N -мерном линейном пространстве, каждая из которых является, в свою очередь, элементом линейного пространства A. В этом случае скалярное произведение (1) определяется как
Знак + используется для обозначения т.н. эрмитовского сопряжения, которое в случае конечномерных пространств представляет собой сочетание двух действий: комплексного сопряжения и транспонирования (превращение столбцов в строки и наоборот). Смысл абстрактных векторов
и вектор-столбцы
перемножая их слева направо по правилу «строка на столбец». Однако, все это уже, в принципе, заложено в символах
Тогда, например, свойство (1¢) может быть получено путем естественного применения операции эрмитового сопряжения +, понимаемой как сочетание операции комплексного сопряжения и транспонирования в смысле, определенном в (6).
Учебные вопросы
1. Сформулируйте определение скалярного произведения волновых функций. 2. Дайте определение нормы волновой функции. 3. Как вводятся в рассмотрение абстрактные векторы состояния Дирака (кэт- и бра-векторы)? 4. Как обобщается понятие скалярного произведения на случай многокомпонентных собственных функций?
|

 , (1)
, (1) ,
,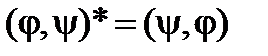 . (1¢)
. (1¢)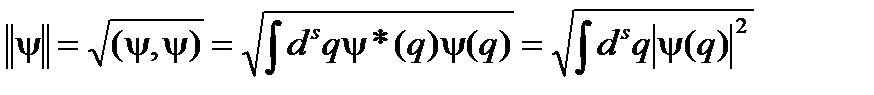 , (2)
, (2)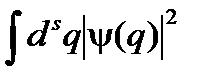 положителен везде в области определения функции y(q) и обращается в ноль только при y(q) = 0.
положителен везде в области определения функции y(q) и обращается в ноль только при y(q) = 0. причем
причем 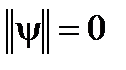 тогда и только тогда, когда y = 0;
тогда и только тогда, когда y = 0; ; (3)
; (3) (неравенство треугольника).
(неравенство треугольника). над полем комплексных чисел C, такое, что свертка его с вектором
над полем комплексных чисел C, такое, что свертка его с вектором 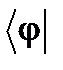 из сопряженного абстрактного пространства Abra будет давать скалярное произведение (1)
из сопряженного абстрактного пространства Abra будет давать скалярное произведение (1) . (4)
. (4) можно представлять себе как результат скалярного произведения бра-вектора
можно представлять себе как результат скалярного произведения бра-вектора 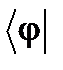 на кэт-вектор
на кэт-вектор 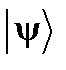 :
: 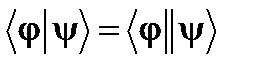 .
.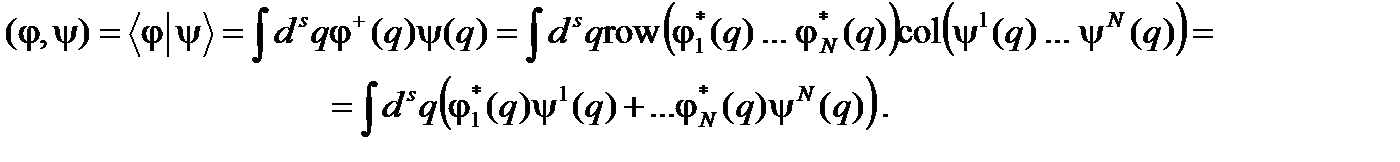 (5)
(5)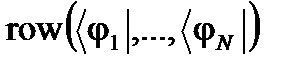
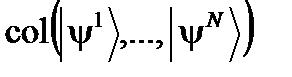 ,
, . (6)
. (6)


