Линейные операторы
8. Пусть A и B – некоторые комплексные линейные пространства. Линейным оператором, отображающим функции yÎ A в функции jÎ B называется оператор
такой, что выполняются условия
для любых функций y1 и y2 и любого комплексного числа l. Если B = A, то оператор 9. Среди всех автоморфизмов в L A существует тождественное преобразование, т.е. преобразование, не меняющее элементов линейного пространства A, описывается единичным оператором, который будем обозначать 10. Простейшие примеры линейных операторов. 11.1. Оператор умножения на некоторую скалярную функцию координат f (q): j(q) = f (q)y(q). (9) 11.2. Оператор дифференцирования по обобщенной координате qi:
11.3. Интегральный оператор
где L (q, q ¢) – ядро интегрального оператора. Многие операторы можно представить в виде интегральных операторов. В частности, единичный оператор
где d(q – q ¢) – многомерная дельта-функция d(q – q ¢) = d(q 1 – q ¢ 1)…d(q s – q ¢ s). (13) Она является ядром единичного оператора. Многомерная дельта-функция может быть корректно определена, если в качестве обобщенных координат выбраны такие, для которых координатный объем dsq совпадает с физическим, т.е. если якобиан преобразования от декартовых координат к обобщенным может быть разбит на соответствующие сомножители, являющиеся функциями отдельных обобщенных координат. В противном случае запись (12) не имеет смысла. С учетом этих оговорок оператор (9) умножения на функцию f (q) (9) также может быть представлен в интегральном виде (11). В этом случае ядром интегрального оператора будет обобщенная функция f (q ¢)d(q – q ¢). Т.о. оператор умножения на функцию есть не что иное, как единичный оператор, умноженный на числовое значение функции: 11. Следует различать правое и левое действия оператора, например, вместо (7) писать:
Стрелочка над оператором показывает направление его действия. Ее надо использовать, чтобы отличить эту запись, в которой 12. При использовании абстрактных кет- и бра-векторов действие линейного оператора может быть определено лишь абстрактно. При этом можно сохранить формальное буквенное обозначение оператора, не нарушая общности записи, например, вместо (7) можно писать
сохраняя то же самое символическое обозначение оператора. Однако при этом далеко не все операторы можно записывать в явном виде. Например, запись (9) оператора умножения на функцию f (q) не может быть явно перенесена на кет-векторы, именно, запись
бессмысленна. 13. Если состояние y непрерывно изменяется с изменением некоторого параметра t, например, со временем: y = y(t), то имеет смысл говорить о зависимости от параметра t соответствующих кет-, или бра-векторов, используя обозначения:
в том смысле, что для любых непрерывно дифференцируемых по t функций
а, с другой стороны, рассматривая
14. На множестве автоморфизмов L A можно ввести произведение операторов
В общем случае
Выражение
называется коммутатором операторов Основные свойства коммутатора операторов:
15. Наряду с коммутатором операторов
Очевидно, Основные свойства антикоммутатора операторов:
16. Операция умножения линейных операторов превращает множество L A линейных операторов над линейным пространством A в т.н. линейную алгебру. Множество этих операций можно символически представить в виде некоторого отображения A ´ A ® A. Такого рода отображение называется бинарным отображением, или бинарной операцией. Коммутатор и антикоммутатор операторов можно рассматривать как некоторую бинарную операцию, обладающую свойством дистрибутивности. Если на множестве линейных операторов вместо обычного их умножения, определенного в п. 16, ввести умножение по правилу (17), т.е. считать, что произведением операторов является коммутатор операторов, то полученная таким образом алгебра операторов называется алгеброй Ли. Если в качестве операции умножения операторов используется антикоммутатор, то говорят об алгебре Иордана. 17. Оператор
Существование обратного оператора зависит от вида оператора и свойств волновых функций, на которые он действует. Если существует обратный оператор 18. Операторы
19. В частном случае, когда
Преобразование подобия переводит произведения операторов, их коммутаторы и антикоммутаторы в операторы, подобные произведению, коммутатору и антикоммутатору операторов соответственно (покажите!). Все возможные преобразования подобия операторов из L A образуют группу, называемую общей линейной группой GL (проверьте выполнение групповых аксиом). 20. Оператор
Очевидно, оператор 21. Оператор
Число p называется степенью нильпотентности оператора. Свойство проективности или нильпотентности оператора не меняется при преобразовании подобия (23) (проверьте!). 22. На основе понятия скалярного произведения функций (1) из всего множества линейных операторов, действующих на A, могут быть выделены различные классы операторов, рассматриваемые ниже. 23. Оператор
24. Оператор
Этот факт символически выражается так
где тильда означает символическую операцию транспонирования. 25. Симметричной частью оператора
26. Оператор
Это свойство символически выражается так
27. Антисимметричной частью оператора
28. Любой оператор
29. Оператор
Сравнивая (35) с (26), с учетом (1¢) можно установить, что можно использовать формальную запись
Очевидно, С помощью операции эрмитового сопряжения даются определения следующих важных классов операторов: эрмитовых операторов, антиэрмитовых операторов и унитарных операторов. 30. Оператор называется эрмитовым, или самосопряженным, если любых функций j и y
Это условие записывают символически в виде
31. Оператор называется антиэрмитовым, или антисамосопряженным, если любых функций j и y
Это условие записывают символически в виде
Антиэрмитовый оператор 32. Аналогично (30) и (31) для произвольного оператора
где Коммутатор эрмитовых операторов 33. Из (34) и (35) видно, что на множестве волновых функций, обладающих свойством (33), оператор ¶ k – антиэрмитов. Тогда оператор – i ¶ k будет эрмитовым оператором. 34. Ядро L +(q, q ¢) интегрального оператора, эрмитово сопряженного к интегральному оператору (11), как видно из непосредственной подстановки (11) в (35) с учетом (1), связано с ядром L (q, q ¢) соотношением (выведите!) L +(q, q ¢) = L *(q ¢, q). (39) Отсюда видно, что ядро эрмитового интегрального оператора характеризуется свойством: L (q, q ¢) = L *(q ¢, q). (40) 35. Произведение эрмитовых операторов
36. Оператор
37. Ядро U (q, q ¢) унитарного интегрального оператора
как можно получить из (41), (39) и (12), обладает следующим свойством (выведите самостоятельно!):
38. Унитарное преобразование сохраняет скалярное произведение волновых функций. Действительно, пусть
39. Пусть функции j и y связаны некоторым оператором 40. Унитарное преобразование сохраняет свойство эрмитовости оператора: если 41. Пусть
42. Определения (26) и (35), а также другие выражения, в которых фигурирует скалярное произведение волновых функций, с учетом (1¢) и (4) могут быть переписаны в символическом виде с помощью кэт- и бра-векторов состояния:
Упражнение: Переписать с помощью кэт- и бра-векторов состояния формулы (27), (29), (36), (37). Указание: принять во внимание правила (6). 43. В дальнейшем, при записи общих результатов теории будут использоваться дираковские обозначения. Выражение
называется матричным элементом оператора 44. Применение понятия матричного элемента к операторам, не являющимся скалярными величинами в пространстве, строго говоря, допустимо лишь для декартовых проекций величин при условии, что само конфигурационное пространство механической системы можно считать евклидовым. В этой связи нельзя также писать в явном виде оператор производной по координате qi от кэт- или бра-вектора. Это же замечание относится и к интегральному оператору (11). 45. Операция транспонирования может оказаться неприменимой на всем множестве волновых функций, заданных в некоторой области конфигурационного пространства. Например, попробуем преобразовать
Если наложить на волновые функции такие граничные условия, чтобы первое слагаемое в (32) обращалось в 0:
где dak – декартовы координаты вектора элемента площади интегрирования по поверхности, охватывающей область определения волновых функций, то из (32) и определения (26) вытекает, что
для любых функций j и y. В каждом конкретном случае выполнение условия (33) требует отдельной проверки (см. п. 118).
Учебные вопросы
1. Что называется оператором? 2. Какие операторы называются линейными операторами? 3. Какой оператор называется автоморфизмом линейного пространства? 4. Что называется ядром интегрального оператора? 5. Какие операторы называются скалярными? Запишите интегральное представление скалярного оператора. 6. Поясните, в чем разница между записью 7. Можно ли применять оператор умножения на функцию обобщенных координат непосредственно к кэт- или бра-векторам? Какие проблемы возникают при попытке непосредственно представить оператор дифференцирования по обобщенным координатам и интегральный оператор в абстрактной записи относительно кэт- или бра-векторов? 8. Можно ли применять в кэт-и бра-векторам, зависящим от параметра, операцию дифференцирования по этому параметру? Если да, то как ее следует понимать? 9. Сформулируйте простейшее понятие произведения операторов? 10. Какое выражение называется коммутатором операторов? Какие операторы называются коммутирующими или перестановочными? 11. Сформулируйте основные свойства коммутатора. 12. Какое выражение называется антикоммутатором операторов? Какие операторы называются антикоммутирующими? 13. Какой оператор называется обратным оператором к данному? Какие операторы называются обратимыми (невырожденными)? 14. Какие операторы называются эквивалентными? 15. Какие операторы называются подобными? 16. Показать, что преобразование подобия переводит произведение операторов в произведение соответствующих им подобных операторов. 17. Показать, что все преобразования подобия образуют группу. 18. Какие операторы называются проективными? Изменяется ли свойство проективности при преобразовании подобия? 19. Какие операторы называются нильпотентными? Что такое степень нильпотентности? Покажите, что свойство нильпотентности не меняется при преобразованиях подобия. 20. Дайте определение транспонированного оператора. 21. Какие операторы называются симметричными (антисимметричными)? Что такое симметричная (антисимметричная) часть оператора? 22. Дайте определение операции эрмитового сопряжения оператора. 23. Какие операторы называются эрмитовыми (самосопряженными)? 24. Какие операторы называются антиэрмитовыми? 25. Покажите, что любой оператор можно представить в виде суммы эрмитовой и антиэрмитовой частей. 26. Покажите, что коммутатор эрмитовых операторов 27. Как найти ядро интегрального оператора, эрмитово сопряженного к исходному интегральному оператору? 28. Какие операторы называются унитарными? Покажите, что унитарные операторы образуют группу U, являющуюся подгруппой группы общих линейных преобразований GL. 29. Каким свойством обладает ядро унитарного интегрального оператора? 30. Как определяется унитарное преобразование операторов? 31. Каково основное свойство унитарного преобразования? 32. Покажите, что свойство эрмитовости оператора сохраняется при унитарном преобразовании. 33. Что называется матричным элементом оператора? 34. Каким образом понятие матричного элемента оператора можно применять к операторам, являющимся нескалярными величинами в пространстве, например, к оператору умножения на координату, или к оператору дифференцирования по координате? 35. Каковы особенности применения операции эрмитового сопряжения к оператору дифференцирования по декартовым координатам?
|

 (7)
(7) (8)
(8) называется автоморфизмом пространства A. Множество всех линейных автоморфизмов пространства A будем обозначать L A. Множество всех автоморфизмов линейного пространства A будем также называть множеством линейных операторов над линейным пространством A.
называется автоморфизмом пространства A. Множество всех линейных автоморфизмов пространства A будем обозначать L A. Множество всех автоморфизмов линейного пространства A будем также называть множеством линейных операторов над линейным пространством A. , или просто 1, если при этом не возникает двусмысленности. Наряду с единичным оператором будем рассматривать нулевой оператор
, или просто 1, если при этом не возникает двусмысленности. Наряду с единичным оператором будем рассматривать нулевой оператор  , который переводит все векторы из A в нулевой вектор. В некоторых случаях, когда это не вызывает недоразумений, его также будем обозначать просто 0.
, который переводит все векторы из A в нулевой вектор. В некоторых случаях, когда это не вызывает недоразумений, его также будем обозначать просто 0. . (10)
. (10)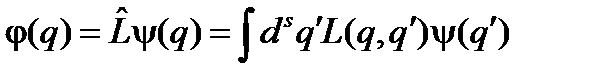 , (11)
, (11) , (12)
, (12) . В этом случае функция f (q ¢) выступает не в качестве элемента линейного пространства A, а в качестве числа, равного значению f (q ¢), из поля чисел, над которым определено пространство A. Такой оператор будем называть скалярным оператором или c - числом (Дирак).
. В этом случае функция f (q ¢) выступает не в качестве элемента линейного пространства A, а в качестве числа, равного значению f (q ¢), из поля чисел, над которым определено пространство A. Такой оператор будем называть скалярным оператором или c - числом (Дирак). . (14)
. (14) является функцией координат, от записи оператора
является функцией координат, от записи оператора  , полученного путем умножения слева на функцию y(q) и действующего обычным образом, слева направо. В приведенных в п. 10 примерах результаты левого и правого действий операторов совпадают. Различия левом и правом действии оператора могут возникнуть в случае, когда речь идет, например, о матрицах, на которые умножаются многокомпонентные функции.
, полученного путем умножения слева на функцию y(q) и действующего обычным образом, слева направо. В приведенных в п. 10 примерах результаты левого и правого действий операторов совпадают. Различия левом и правом действии оператора могут возникнуть в случае, когда речь идет, например, о матрицах, на которые умножаются многокомпонентные функции. , (15)
, (15)
 . В этом случае можно говорить о производной
. В этом случае можно говорить о производной

 как произведение векторов
как произведение векторов 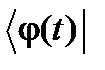 и
и  , можно получить
, можно получить .
. и
и 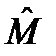 друг на друга как оператор из L A, обозначаемый
друг на друга как оператор из L A, обозначаемый  , и определяемый как результат последовательного действия сначала оператора
, и определяемый как результат последовательного действия сначала оператора 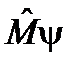 – оператора
– оператора  . (16)
. (16)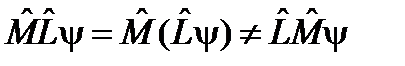 .
. (17)
(17) (антисимметричность)
(антисимметричность) (дистрибутивность) (18)
(дистрибутивность) (18)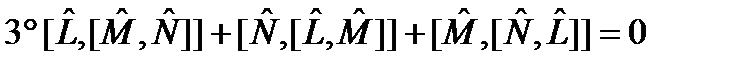 (тождество Якоби)
(тождество Якоби) . (19)
. (19) .
. (симметричность)
(симметричность) (дистрибутивность) (20)
(дистрибутивность) (20)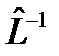 называется обратным оператором к оператору
называется обратным оператором к оператору 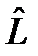 , если выполняются условия
, если выполняются условия . (21)
. (21) , то можно показать, что он является единственным для данного оператора
, то можно показать, что он является единственным для данного оператора  . Оператор
. Оператор  и
и  называются эквивалентными, если существуют два невырожденных оператора
называются эквивалентными, если существуют два невырожденных оператора  и
и  , таких, что
, таких, что . (22)
. (22) , преобразование эквивалентности (22) называется преобразованием подобия:
, преобразование эквивалентности (22) называется преобразованием подобия: . (23)
. (23) называется проективным (идемпотентным), если
называется проективным (идемпотентным), если . (24)
. (24) также будет проективным оператором.
также будет проективным оператором. называется нильпотентным, если существует такое натуральное число p, для которого
называется нильпотентным, если существует такое натуральное число p, для которого . (25)
. (25)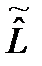 называется оператором, транспонированным к оператору
называется оператором, транспонированным к оператору  , если для любых функций j и y выполняется равенство
, если для любых функций j и y выполняется равенство . (26)
. (26) называется симметричным оператором, если для любых функций j и y выполняется равенство
называется симметричным оператором, если для любых функций j и y выполняется равенство . (27)
. (27)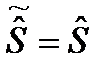 , (27¢)
, (27¢) называется выражение
называется выражение . (28)
. (28)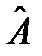 называется антисимметричным оператором, если для любых функций j и y выполняется равенство
называется антисимметричным оператором, если для любых функций j и y выполняется равенство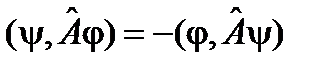 . (29)
. (29) . (29¢)
. (29¢) . (30)
. (30) . (31)
. (31) называется эрмитово сопряженным, или просто сопряженным к оператору
называется эрмитово сопряженным, или просто сопряженным к оператору  , если для любых функций j и y выполняется равенство
, если для любых функций j и y выполняется равенство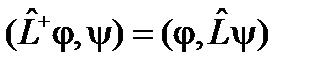 . (35)
. (35) . (35¢)
. (35¢) .
. . (36)
. (36) . (36¢)
. (36¢) . (37)
. (37) . (37¢)
. (37¢)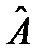 всегда можно получить из некоторого эрмитовского оператора
всегда можно получить из некоторого эрмитовского оператора  путем умножения на
путем умножения на  :
:  .
.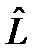 можно ввести понятие эрмитовой и антиэрмитовой части соответственно:
можно ввести понятие эрмитовой и антиэрмитовой части соответственно: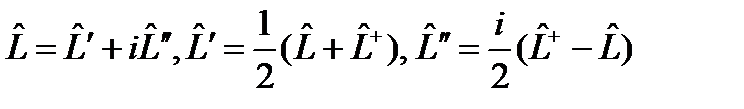 , (38)
, (38) и
и  – эрмитовые операторы, построенные из оператора
– эрмитовые операторы, построенные из оператора  .
. и
и  является антиэрмитовым оператором (докажите!).
является антиэрмитовым оператором (докажите!). и
и  будет эрмитовым оператором тогда и только тогда, когда эти операторы коммутируют:
будет эрмитовым оператором тогда и только тогда, когда эти операторы коммутируют: .
. называется унитарным, если
называется унитарным, если . (41)
. (41) ,
, . (42)
. (42) . Тогда в соответствии с (35)
. Тогда в соответствии с (35) .
. :
:  . Установим вид оператора
. Установим вид оператора  , связывающего унитарные образы этих же функций
, связывающего унитарные образы этих же функций  . для этого представим условие
. для этого представим условие  , откуда следует, что
, откуда следует, что  . Так как оператор
. Так как оператор  унитарен, то это преобразование является частным случаем преобразования подобия (24).
унитарен, то это преобразование является частным случаем преобразования подобия (24).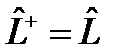 , то
, то  .
.
 , (26¢)
, (26¢) . (35¢ ¢)
. (35¢ ¢) (43)
(43) к виду
к виду  , где ¶ k – оператор дифференцирования по декартовым координатам xk:
, где ¶ k – оператор дифференцирования по декартовым координатам xk: (32)
(32) , (33)
, (33) (34)
(34) .
.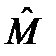 и
и  является антиэрмитовым оператором.
является антиэрмитовым оператором.


