Основы теории представлений. Непрерывный спектр
69. У эрмитовых операторов с непрерывным спектром, вообще говоря, нет полной системы ортонормированных собственных функций y(q, l) (векторов состояния 70. В частности, будем считать, что разложение некоторой волновой функции по собственным функциям y(q, l) эрмитового оператора
существует и единственно на спектре оператора
где d(l – m) – дельта-функция Дирака. Сравнивая с (56), замечаем, что она играет роль символов Кронекера в случае непрерывного спектра. Формулу (69) при заданных собственных функциях y(q, l) некоторого эрмитового оператора можно рассматривать так же, как и (59), как некоторое представление дельта-функции. В формуле (68) пределы интегрирования взяты от – ¥ до ¥, исходя из допущения, что, если область изменения параметра l не совпадает со всей действительной числовой осью, то вне этой области собственные волновые функции оператора обращаются в нуль. Обратное преобразование
определяет непрерывное множество функционалов, образуемых как скалярное произведение функций y(l, q) и f (q). Подстановка (70) в (68)
дает
71. Если скалярное произведение (70) конечно для любого l и любого вектора состояния
где векторы состояния
Предполагается, если это не оговорено особо, что данный интеграл равномерно сходится для любых векторов состояния 72. Понимая интегрирование векторов состояния именно таким образом, можно перенести результаты, полученные для дискретного спектра, mutatis mutandis[2] на непрерывный спектр. Составим таблицу, в которой сопоставлены отдельные результаты теории эрмитовых линейных операторов с дискретным и с непрерывным спектром.
Таблица 1. Основные соотношения теории представлений
73. Если спектр оператора
содержит волновые функции, принадлежащие ортогональным семействам, а именно, кроме условий ортонормировки, имеем:
В дальнейшем, общие выкладки будем производить для простоты в случае дискретного спектра. Обобщение на случай непрерывного спектра представляется не сложным при соблюдении соответствующих условий сходимости. 74. Если операторы
Действуя произведением
т.е. результаты действия операторов 75. Докажем, что, если коммутатор эрмитовых операторов Пусть
Отсюда следует, что, если собственные значения оператора 76. Если для эрмитова оператора
то собственные значения оператора Доказательство этого утверждения может быть проведено следующим образом. Пусть все рассматриваемые операторы имеют дискретный спектр. Так как операторы
Рассмотрим разложение произвольного вектора состояния
Используя эти разложения, вычислим матричный элемент
Если предположить, что спектр оператора
что противоречит третьему условию в (74). Следовательно, предположение о невырожденности спектра оператора 77. Следом оператора называется след представляющей его матрицы:
Если спектр оператора
Чтобы избежать возможных трудностей определения понятия «диагональный элемент оператора» в непрерывном спектре в (78¢) рассматривается предел, к которому стремятся матричные элементы оператора M kl в пределе при k ® l. Сформулированные определения следа оператора являются формальными и требуют уточнения в конкретных случаях. 78. Например, след интегрального оператора (11) можно найти из общего определения следа оператора (78) или (78¢) с учетом условия ортонормировки собственных функций в следующем виде:
Поэтому след интегрального оператора существует, если интеграл, стоящий в правой части (79) сходится. 79. Формальное определение следа оператора, данное выше, обладает рядом свойств, аналогичным свойствам следа матрицы. В частности,
для любого числа m и любых операторов
для любых операторов След оператора является линейным функционалом, заданным на множестве операторов. 80. Из (82) вытекает утверждение: следы операторов, связанные между собой преобразованием подобия (23) совпадают. Действительно, вычислим след правой части (23):
что и доказывает сделанное утверждение. 81. В частности, операторы, связанные друг с другом унитарным преобразованием, имеют одинаковый след. Так как переход между представлениями является унитарным преобразованием, то след оператора не зависит от выбора представления. 82. Эрмитов оператор, имеющий дискретный спектр, унитарным преобразованием сводится к диагональному виду. Поэтому достаточно рассчитать след в собственном представлении оператора. Из таблицы 1, п. 10.1 и определения (78) следует, что след эрмитового оператора, имеющего дискретный спектр, равен сумме его собственных значений
тот результат позволяет уточнить смысл следа эрмитового оператора. След эрмитового оператора, имеющего дискретный спектр, определен, если сходится ряд, стоящий в правой части (83). 83. В случае непрерывного спектра вычисление следа эрмитового оператора через его представление в собственном базисе в общем виде оказывается проблематичным. Вычислим сначала матричные элементы эрмитового оператора, имеющего непрерывный в соответствии с представлением, приведенным в третьем столбце таблицы 1, п. 10.1:
В соответствии с определением (78¢) след оператора, имеющего непрерывный спектр, должен задаваться интегралом
84. След единичного оператора, как видно из (84), либо (79) и (12), (13) в непрерывном спектре оказывается бесконечным. Этот же вывод можно сделать и в случае дискретного спектра на основании (83), если число собственных состояний, образующих базис, счетно. 85. Действие оператора
что эквивалентно символической записи
Если линейное пространство функций A дополнить множеством всех обобщенных функций, к которым относится и дельта-функция Дирака, то запись (85) можно трактовать как задачу на собственные значения и собственные функции оператора координаты, рассматривая дельта-функции d(x – x ¢) как собственные функции этого оператора, а значения координаты – как собственные значения. Такое представление называется координатным представлением. В этом представлении волновые функции y(q) согласно записи (12) представляются в виде разложения по «базису» d(x – x ¢) с коэффициентами разложения, равными y(x ¢).
Учебные вопросы
1. Запишите условие нормировки волновых функций (векторов состояния) эрмитового оператора в дискретном спектре. 2. Как определяется разложение любых волновых функций (векторов состояния) по собственным функциям (векторам состояния) эрмитовых операторов, имеющих дискретный спектр. 3. Покажите, что для собственных функций y n оператора 4. Покажите, что ядро эрмитового интегрального оператора представимо через его собственные значения и собственные функции в виде 5. Покажите, что с помощью собственных векторов состояния 6. Покажите, что любое слагаемое суммы 7. Как записывается действие оператора на функцию (вектор состояния) при разложении по базису собственных функций (векторов состояния) некоторого эрмитового оператора? 8. Как можно определить действие любого оператора в пространстве векторов состояния по его матричным элементам в дискретном спектре? 9. Как будет записываться свойство эрмитовости оператора на языке матричных элементов? 10. Как можно представить оператор, имеющий дискретный спектр, в собственном базисе? 11. Докажите, что собственные числа оператора, возведенного в степень n, будут равны степеням n собственных чисел исходного оператора. 12. Сформулируйте понятие представления. 13. Как связаны базисы и координаты функций (собственных векторов) в них, отнесенные к различным представлениям? Для каких операторов это возможно установить? 14. В чем состоят особенности обобщения теории представлений на непрерывный спектр. Запишите основные соотношения (разложение функций или векторов состояния в непрерывном спектре, обобщение условия ортонормировки на непрерывный спектр, представление действия оператора в непрерывном спектре и т.п.). 15. Показать, что для того, чтобы эрмитовы операторы имели общую систему собственных функций, необходимо и достаточно, чтобы их коммутатор был равен нулю. 16. Показать, что, если для эрмитова оператора 17. Дайте определение следа оператора. 18. Чему равен след оператора в дискретном спектре? 19. Какие проблемы возникают при определении следа оператора в непрерывном спектре? 20. Как установить правило расчета следа интегрального оператора? 21. Что называют координатным представлением? Как в этом представлении можно представить разложение волновых функций по базису?
|

 ). Однако, оказывается, что собственные функции (вектора состояния) оператора
). Однако, оказывается, что собственные функции (вектора состояния) оператора  с непрерывным спектром могут быть выбраны таким образом, что выполняются соотношения, аналогичные полученным выше для случая дискретного спектра.
с непрерывным спектром могут быть выбраны таким образом, что выполняются соотношения, аналогичные полученным выше для случая дискретного спектра. (68)
(68) , (69)
, (69) (70)
(70)
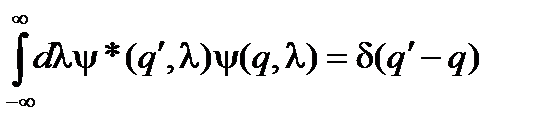 . (71)
. (71) , то (68) можно переписать в следующем символическом виде:
, то (68) можно переписать в следующем символическом виде: , (68¢)
, (68¢) можно рассматривать как функции параметра l, а интегральную сумму в правой части (68¢) – как символическую запись того, что после скалярного умножения (68¢) на произвольный вектор состояния
можно рассматривать как функции параметра l, а интегральную сумму в правой части (68¢) – как символическую запись того, что после скалярного умножения (68¢) на произвольный вектор состояния  предел, к которому стремится бесконечная сумма элементов вида
предел, к которому стремится бесконечная сумма элементов вида  будет несобственным интегралом
будет несобственным интегралом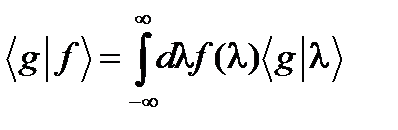 .
.
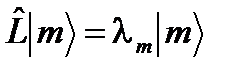





 ;
;



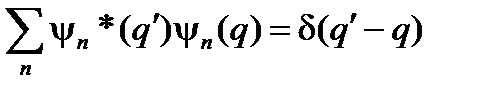
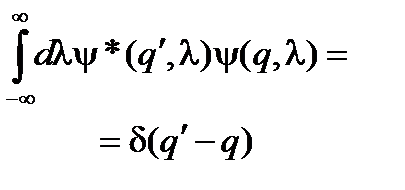






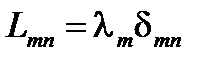

 в базисе собственных функций оператора
в базисе собственных функций оператора 


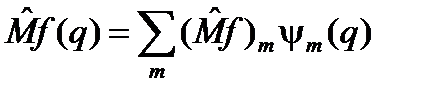
 ;
;
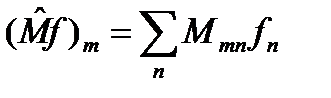
 ;
;
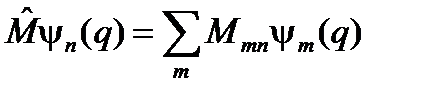


 ;
;

 ;
;

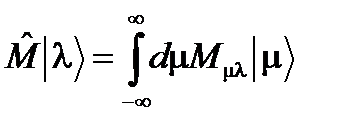




 (72)
(72)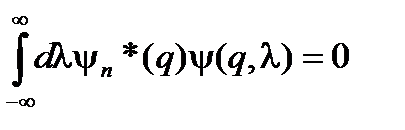 . (73)
. (73) и
и  имеют общую систему собственных функций (собственных векторов), то они коммутируют. Действительно, для любого собственного вектора
имеют общую систему собственных функций (собственных векторов), то они коммутируют. Действительно, для любого собственного вектора  , отвечающего собственному значению ml для оператора
, отвечающего собственному значению ml для оператора  и собственному значению nl для оператора
и собственному значению nl для оператора  , имеем:
, имеем:
 на произвольный вектор состояния
на произвольный вектор состояния  , записанный в разложении по собственным векторам операторов
, записанный в разложении по собственным векторам операторов 
 на произвольные вектора состояния совпадают. Утверждение доказано.
на произвольные вектора состояния совпадают. Утверждение доказано. и
и 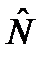 равен нулю, то эти операторы имеют общую систему собственных векторов.
равен нулю, то эти операторы имеют общую систему собственных векторов. в матричном виде с учетом диагональности матричных элементов Mkl запишется следующим образом:
в матричном виде с учетом диагональности матричных элементов Mkl запишется следующим образом: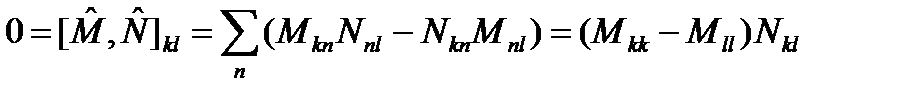 .
. , комплексно сопряженных друг к другу. Из собственных векторов состояния, отвечающих данному собственному значению оператора
, комплексно сопряженных друг к другу. Из собственных векторов состояния, отвечающих данному собственному значению оператора  найдутся эрмитовы операторы
найдутся эрмитовы операторы 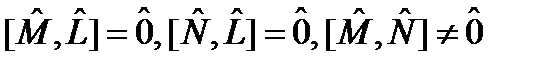 , (74)
, (74)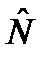 и
и  (75)
(75)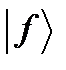 по базисам этих функций, как собственных функций оператора
по базисам этих функций, как собственных функций оператора 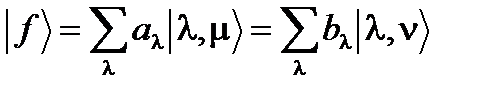 . (76)
. (76) :
: (77)
(77) и
и  ортогональны друг к другу, а скалярное произведение
ортогональны друг к другу, а скалярное произведение  независимо от значений m и n. В этом случае в правой части суммы (77) остаются только слагаемые с одинаковыми l и в силу единственности разложения вектора по базису в (76)надо положить a l = b l:
независимо от значений m и n. В этом случае в правой части суммы (77) остаются только слагаемые с одинаковыми l и в силу единственности разложения вектора по базису в (76)надо положить a l = b l: ,
, . (78)
. (78) . (78¢)
. (78¢)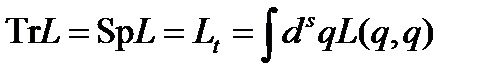 . (79)
. (79) (80)
(80) и
и  (след обладает свойством линейности);
(след обладает свойством линейности); , (81)
, (81)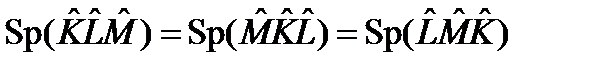 (82)
(82) . Доказательство справедливости этих свойств следа оператора предлагается в качестве самостоятельного упражнения.
. Доказательство справедливости этих свойств следа оператора предлагается в качестве самостоятельного упражнения. ,
, . (83)
. (83)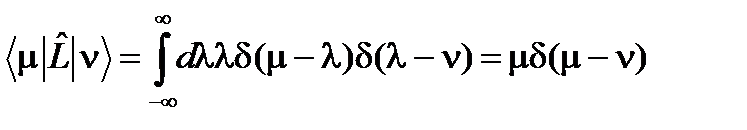 .
.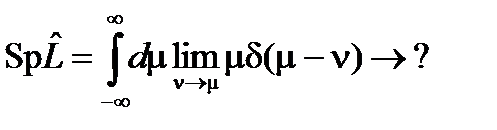 (84)
(84) умножения на декартову координату xi в соответствии со сказанным в п. 11.3 можно представить следующим образом:
умножения на декартову координату xi в соответствии со сказанным в п. 11.3 можно представить следующим образом: ,
, . (85)
. (85) некоторого эрмитового оператора, имеющего дискретный спектр, можно представить действие единичного оператора на пространстве всех векторов состояния в виде
некоторого эрмитового оператора, имеющего дискретный спектр, можно представить действие единичного оператора на пространстве всех векторов состояния в виде  .
. , либо часть ее обладают свойствами проективного оператора.
, либо часть ее обладают свойствами проективного оператора.


