Среднее значение оператора. Соотношения между среднеквадратичными значениями некоммутирующих операторов
86. Средним значением оператора
Эту величину по аналогии с теорией случайных величин называют еще математическим ожиданием оператора 87. Оператор
88. Рассмотрим эрмитов оператор
89. Если векторы
Если среднее значение (87) вычисляется в одном из собственных состояний
т.е. среднее значение оператора в собственном состоянии равно соответствующему собственному значению. 90. В частном случае, когда
Сходимость ряда, стоящего в правой части (89), является условием существования разложения (57¢). В этом случае без нарушения общности можно рассматривать только такие состояния, для которых
Это условие называется условием нормировки вектора состояния (волновой функции). Оно может быть строго обосновано только, если имеет место разложение (57¢). Сравнение (89) и (90) показывает, что, если вектор состояния
91. В случае, когда вектор состояния
то среднее значение оператора
92. Если
В случае, когда интеграл, стоящий в правой части (93), сходится, можно наложить на векторы состояния
Таким образом, понятия нормировки волновой функции в непрерывном спектре и понятия среднего значения оператора, определение матричных элементов оператора и т.п. требуют дополнительного анализа. Эти проблемы удается рассмотреть под другим углом зрения с помощью понятия волнового пакета. 93. Волновым пакетом ширины Dl в спектре оператора
составленное из собственных функций y(q, x) оператора Понятие волнового пакета возникает естественным образом, если интегральное представление (68) записать явно с помощью определения интеграла Римана:
Вводя понятие инфинитезимального волнового пакета
запись (68), (95) можно трактовать так:
Таким образом, разложение функций по волновым пакетам, составленным из собственных функций некоторого эрмитового оператора, имеющего непрерывный спектр, равносильно разложению этой функции по собственным функциям этого оператора. 94. Скалярное произведение произвольных волновых пакетов определяется так же, как и скалярное произведение волновых функций:
где вектор состояния
Если на собственные функции (векторы состояния) накладывается условие (69), то в (97) можно проинтегрировать по всему конфигурационному пространству, получив:
Величина двойного интеграла в (98) при конечных Dl и Dl¢ всегда конечна. Чтобы это показать, рассмотрим следующие случаи. 1) Если отрезки интегрирования в (98) не перекрываются, то в силу свойств дельта-функции
т.е. волновые пакеты с непересекающимися областями определения ортогональны. 2) Если один из отрезков
3) Наконец, если эти отрезки имеют общий отрезок перекрытия:
то результат интегрирования в (98) равен ширине отрезка перекрытия b – a. В случае, когда
a = l - Dl/2, b = l¢ + Dl¢ /2, так что эта ширина равна l¢ - l + Dl¢ /2 + Dl/2. Если же
то a = l¢ – Dl¢ /2, b = l + Dl/2, и ширина отрезка перекрытия составит l - l¢ + Dl¢ /2 + Dl/2. Таким образом, во всех случаях перекрытия областей определения волновых пакетов их скалярное произведение равно ширине области перекрытия, которая всегда конечна:
95. Нормировка волновых пакетов, составленных из собственных функций оператора
С помощью понятия волнового пакета, составленного из собственных функций оператора
В частности, для самого оператора
Вычисление интеграла в (102) необходимо проводить для следующих трех отдельных случаев, рассмотренных в п. 95. 1) Если отрезки 2) Если один из отрезков
3) Если отрезки
где a и b определены в п. 95. Таким образом, во всех случаях данные матричные элементы будут иметь конечные значения. Если ввести в рассмотрение среднее значение оператора
то для самого оператора
Этот результат достигается только при вычислении пакетного среднего значения, тогда как среднее значение оператора в любом из собственных состояний, соответствующих собственным значениям из непрерывного спектра, как было показано в п. 93, по крайней мере, не может быть конечным. В то же время это исчисление не удается развить непротиворечивым образом на произведение операторов и, в частности, на операторы, возведенные в некоторую степень. Так, например, нельзя представить пакетный матричный элемент произведения операторов как сумму произведений пакетных матричных элементов сомножителей, аналогичную действиям с обычными матричными элементами произведения операторов, выписанными в строке 8 таблицы 1. Чтобы это показать, рассмотрим пакетный матричный элемент произведения операторов
Отсюда видно, что переход к пакетным матричным элементам вида (101) для операторов Таким образом, понятие пакетного среднего не дает возможности построить самосогласованный вычислительный аппарат в случае непрерывного спектра. Поэтому понятие волнового пакета широко не используется в литературе. Тем не менее, с этим понятием связаны некоторые эвристические представления, которые имеют определенное хождение особенно среди экспериментаторов и инженеров. О них будет сказано во второй части данного пособия, где будут рассмотрены операторы физических величин. 96. Покажем, что унитарное преобразование операторов и волновых функций не меняет среднего значения оператора. Пусть
где
Полученный результат доказывает сделанное выше утверждение. В частности, если оператор 97. Рассмотрим произвольный, не обязательно эрмитовый, оператор
Действительно, пусть
при любых Если некоторый оператор
если существуют интегралы Аналогичные рассуждения, однако, нельзя провести применительно к волновым пакетам, так как на пакетные матричные элементы произведения операторов не распространяются действия, аналогичные действиям с обычными с матричными элементами операторов. 98. Среднеквадратичным значением оператора
Среднеквадратичным отклонением, или неопределенностью оператора
99. Пусть коммутатор эрмитовых операторов
Возводя в квадрат обе части неравенства и, избавляясь, тем самым, от – i в правой части:
Поскольку коммутатор эрмитовых операторов Соотношение (109) устанавливает ограничение снизу на значение произведения средних квадратов некоммутирующих эрмитовых операторов:
Этот результат применим и к операторам
Следует иметь в виду, что неравенство (108) является более слабым условием, чем неравенство (109). Но (108) можно применять только к физическим величинам, имеющим одинаковые размерности. Неравенства (109), (109¢) и (110) применимы к операторам физических величин различных размерностей.
|

 в состоянии
в состоянии  называется число вида
называется число вида . (86)
. (86) в состоянии
в состоянии 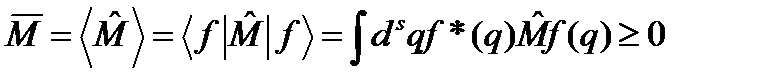 . (87)
. (87) , имеющий дискретный спектр собственных значений l n. Его собственные векторы
, имеющий дискретный спектр собственных значений l n. Его собственные векторы  образуют ортонормированный базис в пространстве векторов состояния. Произвольный вектор состояния
образуют ортонормированный базис в пространстве векторов состояния. Произвольный вектор состояния  . (87)
. (87) . (88)
. (88) , (88¢)
, (88¢) , определение среднего значения (86) сводится к скалярному квадрату волновой функции, описывающей состояние
, определение среднего значения (86) сводится к скалярному квадрату волновой функции, описывающей состояние  , а из правой части (88) для дискретного спектра вытекает, что
, а из правой части (88) для дискретного спектра вытекает, что . (89)
. (89) . (90)
. (90) . (90¢)
. (90¢) эрмитового оператора
эрмитового оператора  , (91)
, (91) . (92)
. (92) – единичный оператор, то из (90) следует, что
– единичный оператор, то из (90) следует, что . (93)
. (93) оказывается неопределенной. В частности, среднее значение
оказывается неопределенной. В частности, среднее значение  , соответствующее собственному значению m, вообще говоря, не определено, т.к. в этом состоянии f (k) = d(k – m),
, соответствующее собственному значению m, вообще говоря, не определено, т.к. в этом состоянии f (k) = d(k – m),  , что в интеграле (92) приводит к выражению
, что в интеграле (92) приводит к выражению .
. называется выражение вида
называется выражение вида , (94)
, (94) на некотором отрезке
на некотором отрезке 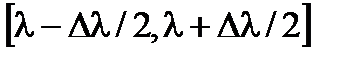 . Отрезок
. Отрезок  (95)
(95) , (96)
, (96) . (95¢)
. (95¢) (97)
(97) надо трактовать в таком же абстрактном смысле, что и векторы состояния, введенные в п. 7. Вектор состояния
надо трактовать в таком же абстрактном смысле, что и векторы состояния, введенные в п. 7. Вектор состояния  , отвечающий инфинитезимальному волновому пакету, в соответствии с (96), (97) связан с собственным вектором состояния
, отвечающий инфинитезимальному волновому пакету, в соответствии с (96), (97) связан с собственным вектором состояния  оператора
оператора  . (96¢)
. (96¢) . (98)
. (98)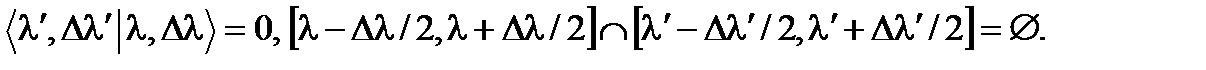
 вложен в другой, то интеграл (А.3) сводится к ширине этого отрезка:
вложен в другой, то интеграл (А.3) сводится к ширине этого отрезка:
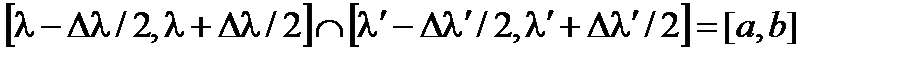 ,
, ,
, ,
, (99)
(99) , (100)
, (100) (101)
(101) (102)
(102)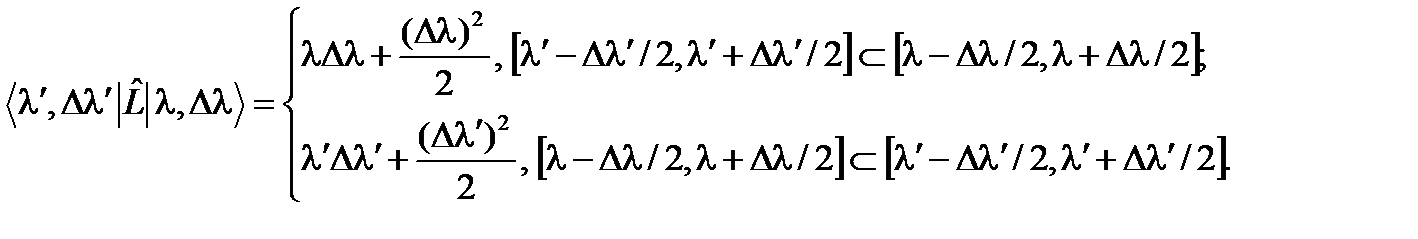 (102.1)
(102.1) , (102.2)
, (102.2) по волновым пакетам оператора
по волновым пакетам оператора  (103)
(103) . (104)
. (104)
 и
и 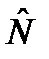 по отдельности невозможен, так как для этого пришлось бы ограничить пределы интегрирования по n до некоторого отрезка конечной длины, что дает только часть соответствующего выражения.
по отдельности невозможен, так как для этого пришлось бы ограничить пределы интегрирования по n до некоторого отрезка конечной длины, что дает только часть соответствующего выражения. ,
, – унитарный оператор, определение которого дано в (41). Среднее значение (86) оператора
– унитарный оператор, определение которого дано в (41). Среднее значение (86) оператора  в состоянии, описываемом волновой функцией
в состоянии, описываемом волновой функцией  :
: .
. , то
, то  не меняется при унитарных преобразованиях.
не меняется при унитарных преобразованиях. . Построим из него оператор
. Построим из него оператор 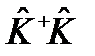 . Этот оператор, очевидно, будет эрмитовым, и, более того, неотрицательно определенным:
. Этот оператор, очевидно, будет эрмитовым, и, более того, неотрицательно определенным: . (105)
. (105)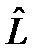 – некоторый эрмитов оператор, имеющий дискретный спектр в пространстве векторов состояния
– некоторый эрмитов оператор, имеющий дискретный спектр в пространстве векторов состояния  . Тогда подстановка (57¢) в выражение для
. Тогда подстановка (57¢) в выражение для 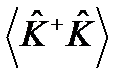 согласно (88) дает:
согласно (88) дает:
 .
. .
. , и интеграл по m сходится. Если сходимость этого интеграла не может быть обеспечена, то все равно, выражение
, и интеграл по m сходится. Если сходимость этого интеграла не может быть обеспечена, то все равно, выражение 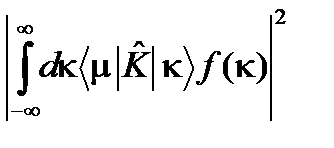 является положительно определенным, хоть и не ограничено.
является положительно определенным, хоть и не ограничено. . (106)
. (106) . (107)
. (107) отличен от нуля:
отличен от нуля:  . Построим оператор
. Построим оператор  . рассмотрим построенный на его основе оператор
. рассмотрим построенный на его основе оператор  . Как показано в п. 97, этот оператор будет эрмитовым и неотрицательно определенным. Из представления
. Как показано в п. 97, этот оператор будет эрмитовым и неотрицательно определенным. Из представления 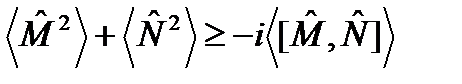 . (108)
. (108) , с учетом очевидного неравенства
, с учетом очевидного неравенства 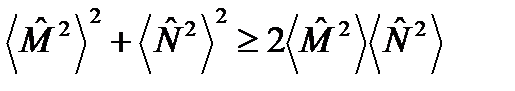 получим:
получим: . (109)
. (109) эрмитов.
эрмитов. . (109¢)
. (109¢) и
и  . Так как коммутатор
. Так как коммутатор  , то из (109¢) в соответствии с определение (107) можно получить соотношение неопределенностей для произвольных некоммутирующих эрмитовых операторов:
, то из (109¢) в соответствии с определение (107) можно получить соотношение неопределенностей для произвольных некоммутирующих эрмитовых операторов: . (110)
. (110)


