Функции от операторов
102. Если
представляет собой оператор, называемый многочленом от оператора. Если многочлен P (z) имеет вещественные коэффициенты, а оператор Собственные значения многочлена от оператора являются соответствующими многочленами от собственных значений оператора. Многочлен P (z) называется аннулирующим многочленом оператора Характеристический многочлен конечномерного оператора равен определителю его l-оператора. 103. Если в некоторой области D комплексной плоскости функция f (z) может быть представлена в виде сходящегося степенного ряда
где ak – комплексные коэффициенты, то формальная подстановка в (114) некоторого оператора
смысл которого зависит от свойств оператора
сходятся в области значений По определению, в разложении (115) считается, что для любого оператора Если коэффициенты разложения ak в (114) вещественны, то функция 104. Если оператор
где натуральное число p является степенью этого многочлена. Подстановка оператора
с помощью которого степень 105. Экспонента от оператора
для любого оператора
сходится абсолютно и равномерно во всей комплексной плоскости чисел z. Поэтому в этом случае условия (115¢) автоматически выполняются. 106. Для произвольных операторов
Равенство 107. Любой обратимый оператор
так как
108. Рассмотрим непрерывное семейство операторов
где x – параметр, а
Рассматривая разложение
при x = 1 можно получить
Это соотношение может быть использовано для вычисления оператора, подобного оператору
Это, в частности, имеет место в случае, когда коммутатор 109. Последнее замечание может быть использовано для нахождения экспоненты от суммы операторов
где
откуда вытекает следующее дифференциальное уравнение для оператора
Если коммутатор
Подставляя (126) в (125), перепишем дифференциальное уравнение для оператора
Так как коммутатор
Таким образом, если коммутатор операторов
Аналогично можно показать, что В частности, при x = 1 из (128) можно получить правило вычисления экспоненты от суммы любых операторов, если их коммутатор перестановочен с каждым из них:
Упражнение. Покажите, что, если коммутатор операторов 110. Любой унитарный оператор
где
111. Производная операторной функции
В частности, производная по
Учебные вопросы и задания: 1. Дайте определение среднего значения оператора. 2. Сформулируйте понятие среднеквадратичного значения оператора и среднеквадратичного отклонения оператора от его среднего значения (неопределенности)? 3. Какие операторы называются неотрицательно определенными? 4. В каких случаях может быть введено условие нормировки волновой функции (вектора состояния)? 5. Дайте определение волнового пакета собственных функций эрмитового оператора. 6. Покажите, что волновые пакеты с непересекающимися областями определения ортогональны. 7. Покажите, что волновые пакеты, имеющие перекрывающиеся области определения, нормируемы на 1. 8. Сформулируйте среднее значение оператора на нормированном волновом пакете. 9. Покажите, что среднее значение оператора на нормированном волновом пакете, составленном из собственных функций этого оператора, равно собственному значению этого оператора, являющегося серединой области определения волнового пакета. 10. Выведите соотношение между средними квадратичными значениями двух эрмитовых операторов в некотором состоянии и их коммутатора в этом же состоянии. Как из этого соотношения получить соотношение неопределенностей? 11. Как определяется зависимость оператора от параметра? Как можно дифференцировать в этом случае операторы по параметру? 12. Дайте определение многочлена от оператора. При каких условиях многочлен от эрмитового оператора будет эрмитовым оператором? 13. Как связаны собственные значения многочлена от оператора и самого оператора? 14. Какой многочлен называется аннулирующим многочленом оператора? 15. Каким образом можно представить произвольную функцию от оператора, и в каких случаях это представление возможно? 16. Покажите, что, если определена некоторая функция от конечномерного оператора, то она сводится к некоторому многочлену степени p – 1, где p – степень минимального многочлена оператора. 17. Как определить экспоненту от оператора? 18. Покажите, что экспонента от оператора является обратимым оператором. 19. Выведите свойство 20. Покажите, что, если для двух операторов 21. Покажите, что любой унитарный оператор может быть представлен в виде 22. Каким образом можно сформулировать определение понятия производной функции от оператора по этому оператору?
Литература
1. Елютин П.В., Кривченков В.Д. Квантовая механика с задачами. М.: Физматлит, УНЦ довузовского образования МГУ, 2001. 2. Боум А. Квантовая механика. Основы и приложения. М.: Мир, 1990. [1] Оператор [2] С соответствующими изменениями (лат.)
|

 – некоторый многочлен степени n с, вообще говоря, комплексными коэффициентами, то для некоторого линейного оператора
– некоторый многочлен степени n с, вообще говоря, комплексными коэффициентами, то для некоторого линейного оператора  выражение
выражение (113)
(113) , (114)
, (114) , (115)
, (115) . Если на множестве векторов состояния
. Если на множестве векторов состояния 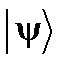 любые матричные элементы
любые матричные элементы  являются числами, лежащими в области D, то представление (104) имеет следующий смысл: числовые ряды
являются числами, лежащими в области D, то представление (104) имеет следующий смысл: числовые ряды , (115¢)
, (115¢) для любых
для любых  и
и  . В этом случае будем считать, что функция от оператора
. В этом случае будем считать, что функция от оператора 
 . Это предположение не противоречит (115¢).
. Это предположение не противоречит (115¢). от эрмитового оператора
от эрмитового оператора  , (116)
, (116)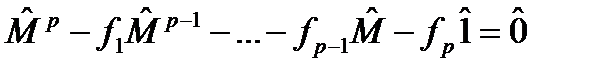 , (117)
, (117) оператора можно выразить через его более низкие степени. Тогда, используя (117), ряд (115) можно свести к операторному многочлену вида (113) степени n = p – 1. Таким образом, любая функция от конечномерного оператора, имеющего минимальный многочлен степени p, представимая в виде сходящегося степенного ряда (114) при выполнении условий (115¢) может быть представлена как некоторый операторный многочлен (113) степени n = p – 1.
оператора можно выразить через его более низкие степени. Тогда, используя (117), ряд (115) можно свести к операторному многочлену вида (113) степени n = p – 1. Таким образом, любая функция от конечномерного оператора, имеющего минимальный многочлен степени p, представимая в виде сходящегося степенного ряда (114) при выполнении условий (115¢) может быть представлена как некоторый операторный многочлен (113) степени n = p – 1. определяется с помощью ряда
определяется с помощью ряда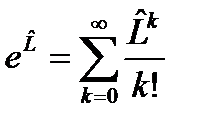 (118)
(118) (119)
(119)
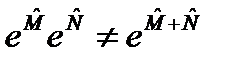 . (120)
. (120) выполняется только тогда, когда операторы
выполняется только тогда, когда операторы  может быть представлен в виде экспоненты от некоторого оператора
может быть представлен в виде экспоненты от некоторого оператора 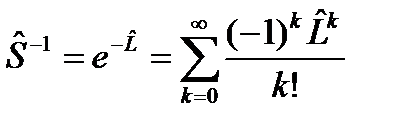 , (121)
, (121) .
. , получаемое из оператора
, получаемое из оператора  ,
, – некоторый оператор. Производные этого оператора по параметру x ведут себя следующим образом:
– некоторый оператор. Производные этого оператора по параметру x ведут себя следующим образом: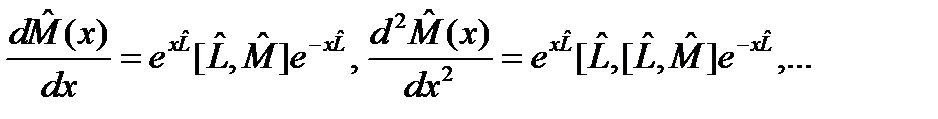 .
.
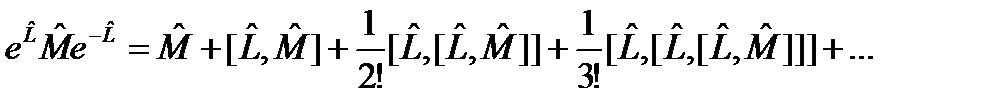 (122)
(122) перестановочен с оператором
перестановочен с оператором  :
: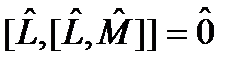 . (123)
. (123) является c -числом (см. п. 11.3). Тогда все коммутаторы
является c -числом (см. п. 11.3). Тогда все коммутаторы 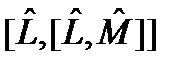 ,
,  и т.д. обращаются в нуль.
и т.д. обращаются в нуль.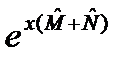 в виде
в виде , (124)
, (124) – некоторый оператор. Чтобы его найти, продифференцируем обе части (124) по x и слева подставим вместо
– некоторый оператор. Чтобы его найти, продифференцируем обе части (124) по x и слева подставим вместо 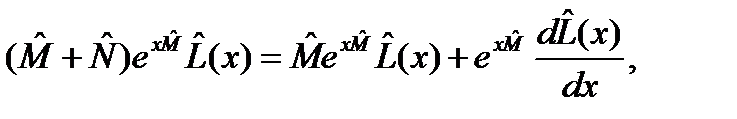
 . (125)
. (125) перестановочен с оператором
перестановочен с оператором  . (126)
. (126) . (127)
. (127)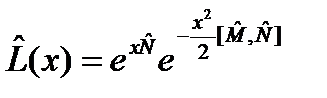 .
. . (128)
. (128) , т.е. роли операторов в правой части (128), как и в левой части, равноправны. Экспоненциальный множитель
, т.е. роли операторов в правой части (128), как и в левой части, равноправны. Экспоненциальный множитель  при этом перестановочен с обеими экспонентами
при этом перестановочен с обеими экспонентами  и
и  , и может быть записан в любом месте произведения, стоящего в правой части (128). В частности, если
, и может быть записан в любом месте произведения, стоящего в правой части (128). В частности, если 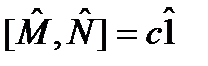 , то
, то  .
. . (129)
. (129)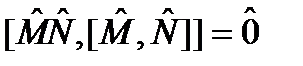 ,
, 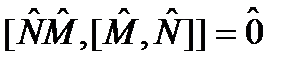 .
.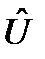 может быть представлен в виде
может быть представлен в виде , (130)
, (130) – некоторый эрмитов оператор. Эрмитовость оператора
– некоторый эрмитов оператор. Эрмитовость оператора 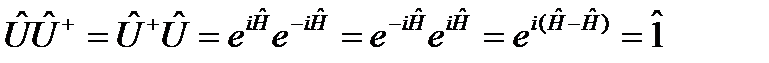 .
. по своему аргументу
по своему аргументу  определяется следующим образом:
определяется следующим образом: . (131)
. (131)
 .
. и
и  справедливы соотношения:
справедливы соотношения:  ,
,  , то
, то  называется резольвентой оператора
называется резольвентой оператора  . Термин «l-оператор» является аналогом понятия l-матрицы в теории матриц.
. Термин «l-оператор» является аналогом понятия l-матрицы в теории матриц.


