Задача на собственные значения и собственные функции линейных операторов
46. Уравнение (система уравнений)
где l – вообще говоря, комплексное число, а y(q) = y(l, q) = yl(q) (45) называется собственной функцией оператора Записи (44) с учетом обозначений (45) можно поставить в соответствие абстрактную запись
где Собственные векторы (функции) оператора определены с точностью до умножения на оператор, коммутирующий с ним, т.е. если Применяя операцию эрмитового сопряжения к уравнению (46), получим, что сопряженные собственные векторы
47. Если существует обратный оператор
т.е. собственные векторы обратного оператора совпадают с собственными векторами исходного оператора, а его собственные значения равны l–1. 48. Собственные значения эрмитовых операторов являются действительными числами. В самом деле, пусть оператор 49. Если
Таким образом, собственные значения унитарных операторов по модулю равны 1: 50. Собственные векторы
С другой стороны, на основании свойства эрмитовости
Разность (49.1) и (49.2)
дает, что при l1 ¹ l2 51. Собственное значение l оператора
где по повторяющемуся сверху и снизу индексу производится суммирование от 1 до p, также будет собственным вектором оператора 52. Если при некотором собственном значении l решение уравнения (46) единственно, то говорят, что это собственное значение невырождено. 53. Согласно утверждению, доказанному в п. 51, собственные векторы, отвечающие различным невырожденным собственным значениям эрмитового оператора, ортогональны между собой. Любой из собственных векторов, соответствующих вырожденному собственному значению, ортогонален собственному вектору, который соответствует невырожденному собственному значению. Собственные векторы 54. Покажем, что в случае конечного числа p собственных векторов состояния существует бесконечное число способов построения линейных комбинаций (50) векторов Рассмотрим p линейных комбинаций вида (50), ортогональных друг к другу:
Для соответствующих бра-векторов по правилам (6) будем иметь:
Потребуем, чтобы векторы
Тогда подстановка (51) и (51¢) в (52) приведет к условиям вида
В системе (53) содержится p (p – 1) вещественных условий для p 2 неизвестных комплексных чисел c a i. Поэтому оставшиеся из них p комплексных чисел будут задаваться произвольно, с единственным лишь ограничением, что определитель матрицы c a i должен быть отличен от нуля: det(c a i) ¹ 0. Одним из наиболее распространенных в литературе способов ортогонализации векторов состояния, отвечающих одному и тому же собственному значению, является метод Грамма – Шмидта. Он применим лишь в случае, когда скалярные произведения Рассмотрим сначала систему двух неортогональных собственных векторов
Потребуем, чтобы векторы
Так как состояния
При кратности вырождения p > 2 рассматривается следующий шаг: строится вектор состояния
в котором коэффициенты 55. Если множество собственных значений оператора
где собственные функции y(m, q) = y m (q) и, соответственно, собственные векторы 56. Если собственное значение l оператора пробегает непрерывный ряд значений в некоторой области комплексной плоскости, то говорят, что оператор имеет непрерывный спектр. Часто оператор может иметь как дискретную, так и непрерывную часть спектра. 57. Понятие о спектре оператора достаточно строго определено только для т.н. ограниченных операторов. Оператор
Наименьшее из чисел M, удовлетворяющее данному условию при любых y, называется нормой оператора Пусть В этих точках: 1) оператор 2) оператор Строго говоря, задача о нахождении собственных векторов и собственных значений оператора корректно формулируется в виде (45), или (46) лишь для дискретной части спектра оператора (если таковая существует). В случае непрерывной части спектра оператора может оказаться, что решения задачи (45) представляют собой функции, норма которых бесконечна, и поэтому оператор Согласно доказанному в п. 49 свойству собственных чисел эрмитового оператора, его спектр лежит на действительной оси в комплексной плоскости чисел l. Все остальные точки комплексной плоскости чисел l являются регулярными точками эрмитового оператора. В соответствии с доказанным в п. 50 спектр унитарного оператора лежит на единичном круге в комплексной плоскости чисел l. Все остальные точки комплексной плоскости чисел l внутри и вне единичного круга являются регулярными точками унитарного оператора. 58. Если слева подействовать невырожденным оператором
показывает, что вектор состояния Согласно п. 44, унитарные преобразования, являющиеся частным случаем преобразований подобия, сохраняют эрмитовость оператора и норму волновой функции. Следовательно, условия, при которых l-операторы операторов
Учебные вопросы:
1. Сформулируйте задачу на собственные значения и собственные функции (векторы состояния) линейного оператора. Однозначно ли решение этой задачи? 2. Какой вид имеют собственные векторы и собственные числа оператора, обратного данному? 3. Покажите, что собственные значения эрмитовых операторов вещественны. 4. Какой общий вид имеют собственные значения унитарных операторов? 5. Покажите, что собственные функции (вектора состояния) ортогональны, если соответствующие им собственные числа различны. 6. Какие собственные значения оператора называются вырожденными? Что такое кратность вырождения собственного значения? 7. Покажите, что в случае конечного значения кратности вырождения собственного числа для него всегда можно подобрать ортогональные линейные комбинации отвечающих ему собственных функций (векторов состояния). 8. Что называется спектром оператора? 9. Как определяется дискретный спектр оператора? 10. Какие операторы называются ограниченными? 11. Как определяется непрерывный спектр оператора? 12. Совокупности собственных значений операторов, подобных друг другу, на первый взгляд, должны совпадать. Почему же все-таки в общем случае нельзя утверждать, что спектры подобных операторов совпадают? При каком виде преобразований подобия они будут совпадать?
|

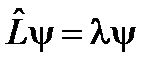 , (44)
, (44)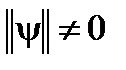 , называется задачей на собственные значения и собственные функции оператора
, называется задачей на собственные значения и собственные функции оператора  . Решение (44)
. Решение (44)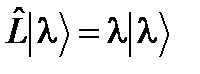 , (46)
, (46)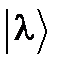 – собственный вектор состояния оператора
– собственный вектор состояния оператора  , то векторы состояния
, то векторы состояния 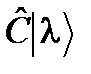 также будут собственными векторами оператора
также будут собственными векторами оператора  , согласно правилам (6), оказываются собственными векторами оператора
, согласно правилам (6), оказываются собственными векторами оператора 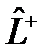 , эрмитово сопряженного к оператору
, эрмитово сопряженного к оператору 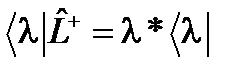 . (47)
. (47)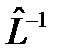 , то, действуя им слева на обе части уравнения (46), найдем, что
, то, действуя им слева на обе части уравнения (46), найдем, что , (48)
, (48)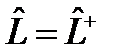 . Умножая (46) скалярно на
. Умножая (46) скалярно на  , а (48) – скалярно на
, а (48) – скалярно на 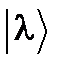 , и вычитая получающиеся равенства одно из другого, найдем, что
, и вычитая получающиеся равенства одно из другого, найдем, что 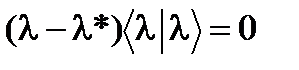 . Т.к. по
. Т.к. по 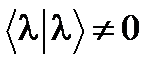 , то l = l*.
, то l = l*.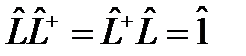 , из (46), (47) и (48) следует, что для любого унитарного оператора
, из (46), (47) и (48) следует, что для любого унитарного оператора .
.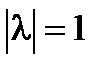 , т.е. могут быть представлены в виде l = ei a.
, т.е. могут быть представлены в виде l = ei a.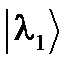 и
и 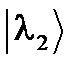 эрмитового оператора
эрмитового оператора 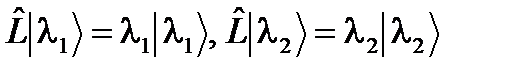 . С одной стороны,
. С одной стороны,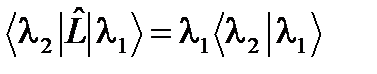 . (49.1)
. (49.1)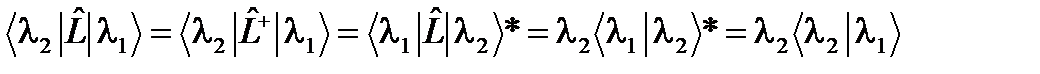 . (49.2)
. (49.2) (49.3)
(49.3)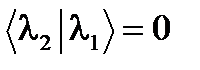 , что доказывает сформулированное утверждение.
, что доказывает сформулированное утверждение. , a = 1, …, p, соответствующих одному и тому же собственному значению l, то число p называется кратностью вырождения собственного значения l. Любая линейная комбинация этих векторов
, a = 1, …, p, соответствующих одному и тому же собственному значению l, то число p называется кратностью вырождения собственного значения l. Любая линейная комбинация этих векторов , (50)
, (50)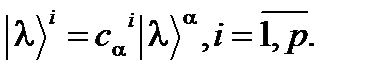 (51)
(51) . (51¢)
. (51¢)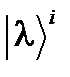 с различными номерами i и j были ортогональны друг к другу:
с различными номерами i и j были ортогональны друг к другу: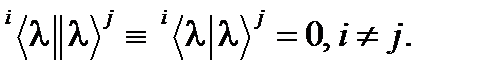
 (52)
(52)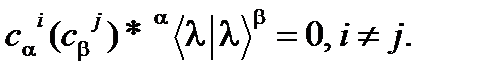
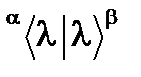 конечны. Его суть заключается в следующем.
конечны. Его суть заключается в следующем.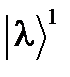 и
и  . Построим из этих векторов пару новых векторов
. Построим из этих векторов пару новых векторов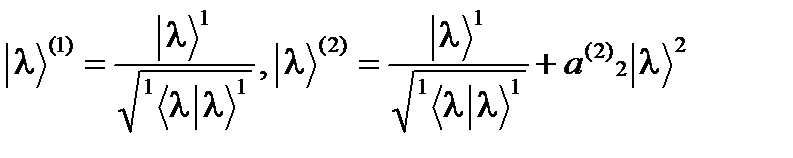 .
.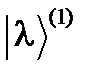 и
и 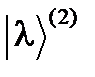 были ортогональны:
были ортогональны: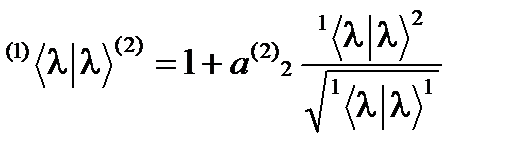 .
.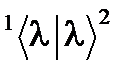 ¹ 0, и для коэффициентов
¹ 0, и для коэффициентов  будем иметь:
будем иметь: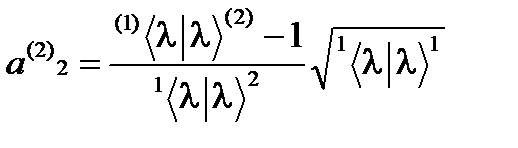 .
.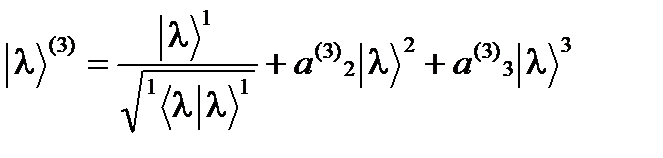 ,
,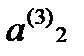 и
и  отыскиваются из условий ортогональности этого вектора векторам
отыскиваются из условий ортогональности этого вектора векторам 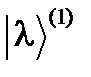 и
и 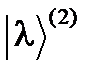 . Продолжая построение таким образом, можно получить систему конечного числа p ортогональных собственных векторов состояния.
. Продолжая построение таким образом, можно получить систему конечного числа p ортогональных собственных векторов состояния.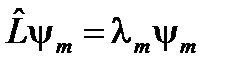 , (54)
, (54) , (55)
, (55) отвечают собственному значению l m.
отвечают собственному значению l m.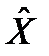 называется ограниченным, если существует такое конечное число M, что для любой функции y из области определения оператора выполняется условие
называется ограниченным, если существует такое конечное число M, что для любой функции y из области определения оператора выполняется условие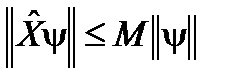 .
.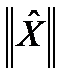 . Можно показать, что норма оператора удовлетворяет условиям, аналогичным условиям (3) для нормы функции.
. Можно показать, что норма оператора удовлетворяет условиям, аналогичным условиям (3) для нормы функции.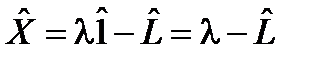 – l-оператор оператора
– l-оператор оператора 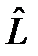 . Значения параметра l, при которых оператор
. Значения параметра l, при которых оператор 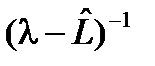 , обратный к l-оператору оператора
, обратный к l-оператору оператора  существует, определен всюду в области определения оператора
существует, определен всюду в области определения оператора 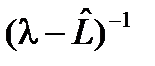 не существует (дискретная часть спектра), либо
не существует (дискретная часть спектра), либо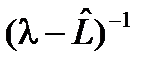 существует, но не определен всюду в области определения оператора
существует, но не определен всюду в области определения оператора 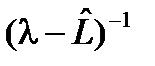 может быть не определен всюду в области определения оператора
может быть не определен всюду в области определения оператора 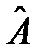 на равенство (46), то следующая цепочка рассуждений
на равенство (46), то следующая цепочка рассуждений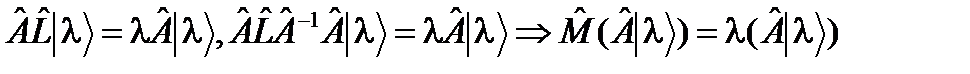 ,
, является собственным вектором оператора
является собственным вектором оператора 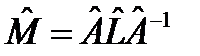 , отвечающим тому же собственному значению l, что и собственный вектор
, отвечающим тому же собственному значению l, что и собственный вектор 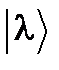 исходного оператора
исходного оператора  . Однако, в общем случае нельзя утверждать, что подобные операторы имеют одинаковый спектр. Для того, чтобы спектры подобных операторов совпадали, необходимо и достаточно, чтобы для обоих операторов условия 1) и 2) выполнялись на одном и том же множестве значений l.
. Однако, в общем случае нельзя утверждать, что подобные операторы имеют одинаковый спектр. Для того, чтобы спектры подобных операторов совпадали, необходимо и достаточно, чтобы для обоих операторов условия 1) и 2) выполнялись на одном и том же множестве значений l.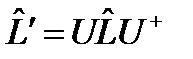 оказываются ограниченными, одинаковы для обоих операторов. Значит, при унитарных преобразованиях множество собственных значений оператора остается неизменным.
оказываются ограниченными, одинаковы для обоих операторов. Значит, при унитарных преобразованиях множество собственных значений оператора остается неизменным.


