Теоретические сведения. Прямую линию с выбранным на ней началом отсчета, единичным отрезком и направлением называют координатной прямой
2.2. Оценка тяжести сочетанных травм
2.3. Феномен взаимного отягощения повреждений при тяжелой сочетанной травме
Прямую линию с выбранным на ней началом отсчета, единичным отрезком и направлением называют координатной прямой. Каждому натуральному числу можно поставить в соответствие единственную точку на координатной прямой. Два числа, отличающиеся друг от друга только знаком, называются противоположными числами. Например, числа 1 и -1, 5 и -5 противоположные. Числа натуральные, им противоположные, а также число нуль составляют множество целых чисел. Оно обозначается Множество натуральных чисел, дополненное нулем, называют множеством целых неотрицательных чисел и обозначают Каждому целому числу можно поставить в соответствие единственному точку координатной прямой. Объединение множеств целых и дробных чисел (положительных и отрицательных) составляет множество рациональных чисел. Его обозначают На множестве Каждому рациональному числу можно поставить в соответствие единственную точку координатной прямой. Сравнение рациональных чисел Из двух чисел то больше, которое на координатной прямой расположено правее. Следовательно: а) всякое положительное число больше нуля и больше отрицательного числа; б) всякое отрицательное число меньше нуля; в) из двух отрицательных чисел больше то, модуль которого меньше. Например, Сложение и вычитание рациональных чисел Сумма двух чисел с одинаковыми знаками равна числу того же знака, модуль которого равен сумме модулей слагаемых. Например, Сумма двух чисел с разными знаками равна числу, модуль которого получается вычитанием из большего модуля меньшего, а знак суммы совпадает со знаком слагаемого, имеющего больший модуль. Например, Сумма противоположных чисел равна нулю. Например, Чтобы вычесть из числа а число b, достаточно к уменьшаемому прибавить число, противоположное вычитаемому. Например, Умножение и деление рациональных чисел Произведение двух чисел одного знака есть число положительное. Например, Произведение двух чисел с разными знаками есть число отрицательное. Например, Аналогично производится деление. Например, Возведение рациональных чисел в степень с натуральным показателем Степенью числа а с показателем k, где
Число а называется основанием степени, а число k — показателем степени. Четная степень отрицательного числа есть число положительное. Например, Нечетная степень отрицательного числа есть число отрицательное. Например, Любая степень положительного числа есть число положительное. Например, При возведении нуля в любую натуральную степень k получается нуль, т. е. При возведении единицы в любую натуральную степень k получается единица, т. е.
|

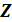 .
. .
.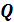 . Любое рациональное число может быть записано в виде
. Любое рациональное число может быть записано в виде  , где
, где  .
.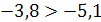 , так как
, так как  .
. .
. .
. .
.
 .
. .
. .
. .
. , называется произведение k множителей, каждый из которых равен а:
, называется произведение k множителей, каждый из которых равен а: .
. .
. .
. .
. .
.


