
Качества оценки определяют, проверяя, обладает ли она свойствами несмещенности, состоятельности и эффективности.
Оценка  параметра
параметра  называется несмещенной, если
называется несмещенной, если 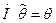 , т.е. математическое ожидание случайной величины
, т.е. математическое ожидание случайной величины  должно быть равно значению параметра
должно быть равно значению параметра  .
.
Оценка 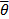 п называется состоятельной, если сходится по вероятности к оцениваемому параметру:
п называется состоятельной, если сходится по вероятности к оцениваемому параметру:  . Это означает, что с увеличением объема выборки мы все ближе к истинному (достоверному) значению
. Это означает, что с увеличением объема выборки мы все ближе к истинному (достоверному) значению  .
.
Несмещенная оценка 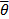 п называется эффективной, если ее дисперсия минимальна.
п называется эффективной, если ее дисперсия минимальна.
Статистическая оценка, используемая в качестве приближенного значения неизвестного параметра генеральной совокупности, называется ее точечной оценкой.
Точечные оценки хороши в качествепервоначальных результатов обработки наблюдений, однако заранее неизвестно с какой точностью они представляют оцениваемый параметр.
В результате возникает задача о приближении параметра  не одним числом, а целым интервалом значений (в частности концами интервала), при этом оценка неизвестного параметра будет называться интервальной, а интервал (
не одним числом, а целым интервалом значений (в частности концами интервала), при этом оценка неизвестного параметра будет называться интервальной, а интервал (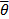 1;
1; 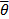 2), накрывающий с вероятностью
2), накрывающий с вероятностью  истинное значение параметра
истинное значение параметра  , - доверительным интервалом и вероятность
, - доверительным интервалом и вероятность  - надежностью оценки или доверительной вероятностью.
- надежностью оценки или доверительной вероятностью.


 параметра
параметра  называется несмещенной, если
называется несмещенной, если 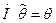 , т.е. математическое ожидание случайной величины
, т.е. математическое ожидание случайной величины 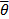 п называется состоятельной, если сходится по вероятности к оцениваемому параметру:
п называется состоятельной, если сходится по вероятности к оцениваемому параметру:  . Это означает, что с увеличением объема выборки мы все ближе к истинному (достоверному) значению
. Это означает, что с увеличением объема выборки мы все ближе к истинному (достоверному) значению  истинное значение параметра
истинное значение параметра 


