Задание 6. Пример 1. Плотность вероятности случайной величины Х равна ,
Пример 1. Плотность вероятности случайной величины Х равна Решение. Согласно свойству плотности непрерывной случайной величины
Следовательно, Пример 2. Плотность вероятности случайной величины Х равна
Найти функцию распределения случайной величины Х и вероятность попадания Х в промежуток Решение. Поскольку все значения случайной величины Х сосредоточены на промежутке
И наконец, Пример 3. Вычислить математическое ожидание случайной величины Х, плотность вероятности которой равна
Решение. Используем формулу для вычисления математического ожидания непрерывных случайных величин:
Вначале найдем первообразную функции
Итак,
|
, 
. Определить константу с.
. Но
.
, 
.
.
, то при 
верно 
, а при 
верно 
, где 
- функция распределения случайной величины Х. Пусть 
. Тогда по определению функции распределения непрерывной случайной величины имеем:
.
.
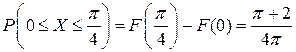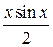методом интегрирования по частям: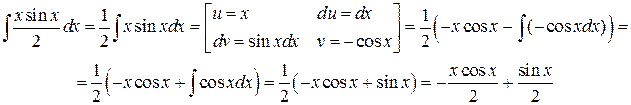
.
