Задание 11. Пример 1. На основании анализа производительности труда 20 человек, выбранных из достаточно большой генеральной совокупности

Пример 1. На основании анализа производительности труда 20 человек, выбранных из достаточно большой генеральной совокупности, было установлено, что среднее квадратическое отклонение суточной выработки составляет 15 кг в час, а выборочная средняя производительность – 620 кг в час. Предполагая, что производительность имеет нормальное распределение, найти границы, в которых с надежностью 0, 9 заключены соответственно средняя суточная производительность всей генеральной совокупности и ее дисперсия.

Решение.

Поскольку объем генеральной совокупности достаточно большой (это сказано в условии), то выборку из 20 человек можно считать повторной. Известно, что если генеральная совокупность имеет нормальное распределение, то доверительные интервалы с надежностью γ соответственно для ее математического ожидания и дисперсии равны

, .

где n – объем повторной выборки, и - соответственно выборочные средняя и дисперсия, - квантиль уровня t -распределения с степенями свободы, - квантиль уровня -распределения с степенями свободы. В нашем случае , , , , . Поэтому искомые доверительные интервалы для генеральных средней и дисперсии соответственно равны (614, 05; 625, 95), (149, 5; 445, 5).

Пример 2. При обследовании выработки рабочих большого завода по схеме собственно-случайной повторной выборки было отобрано 100 рабочих и по этой выборке получены следующие данные: средняя выработка равна 119, 2 %, среднее квадратическое отклонение равно 9, 353 %. Определить границы, в которых с вероятностью 0, 9 заключена средняя выработка рабочих завода; определить объем выборки, при котором с вероятностью 0, 9 отклонение средней выработки рабочих в выборке от средней выработки рабочих завода не превзойдет 1 %.

Решение.

Известно, что для выборок большого объема доверительный интервал с надежностью для генеральной средней приближенно равен

,

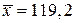где n – объем выборки, и s – соответственно выборочные средняя и дисперсия, - квантиль уровня нормального закона. В нашем случае , , , . Поэтому искомый доверительный интервал равен (117, 67; 120, 73).