Задание 2. Пример 1. В квадрат вписана окружность радиуса R, а в окружность вписан правильный треугольникПример 1. В квадрат вписана окружность радиуса R, а в окружность вписан правильный треугольник. Найти вероятность того, что точка, брошенная наудачу в квадрат, попадет в треугольник. Решение. Вероятность попадания точки в треугольник равна отношению площади треугольника к площади квадрата:
при этом сторона квадрата, описанного около окружности радиуса R, равна 2R, а площадь
Ответ: Пример 2. В цилиндр (радиус основания равен R, высота равна R) вписан конус, основание которого совпадает с основанием цилиндра. Найти вероятность того, что точка, выбранная наугад внутри цилиндра, окажется внутри конуса. Решение. Вероятность попадания точки в конус равна отношению объема конуса к объему цилиндра:
Объем цилиндра, высота которого равна H, а радиус основания R, определяется по формуле Объем конуса, высота которого равна H, а радиус основания R, вычисляется по формуле Ответ:
|
,
; площадь треугольника, вписанного в окружность радиуса R, равна 
. Тогда
.
.
.
, а так как 
, то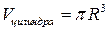 
.
. Т.к. высота конуса равна высоте цилиндра, то для конуса 
. Отсюда 
.
.
