Случайные величины и их характеристики

Величина, которая в зависимости от обстоятельств может принимать различные значения, называется случайной.

Таким образом случайная величина характеризуется возможными значениями, которые она может принимать, и вероятностями, с которыми эти значения принимаются.

Совместное рассмотрение нескольких случайных величин приводит к системам случайных величин (например, координаты точки попадания снаряда, оценки наудачу взятого абитуриента и т.д.).

Существуют дискретные и непрерывные случайные величины, для которых определены соответственно законы или функции распределения, а также принятые на практике числовые характеристики.

 

Дискретные и непрерывные случайные величины (СВ)

 

Закон распределения дискретной случайной величины устанавливает связь между возможными значениями СВ х и соответствующими им вероятностями p, что можно представить в табличном виде:

х1	х2	…	хk
p1	p2	…	pk

 

Функцией распределения непрерывной СВ называется функция

F(x), выражающая вероятность того, что значение случайной величины Х, меньше чем х:

F(x) = .

Плотность вероятности непрерывной СВ: при этом .

Вероятность попадания значения СВ в заданный интервал (а; b):

.

Числовые характеристики СВ:

Математическое ожидание МХ = x_ip_i

или МХ= - среднее значение СВ в центре ее распределения.

Дисперсия (рассеяние) DX = М[(x - MX)²] = (x_i –M(x))²p_i

или - мера рассеяния данной СВпо отношению к ее ожиданию

Среднее квадратичное отклонение: .

 

Пример 14. Дан законраспределения дискретной случайной величины(ДСВ):

 

х
р	0, 1	0, 2	0, 4	0, 2	0, 1

Вычислить математическое ожидание, дисперсию и среднее квадратичное отклонение для заданного распределения, найти моду ДСВ.

Решение: МХ = ∑ x_ip_i = 2 4 0, 2 + 7 0, 4 + 9 0, 2 +11 0, 1 = 6, 7

Для нахождения DХ по соответствующей формуле, вместо (х_i – МХ)² Р_i найдем М(х²) согласно таблице:

 

х
р	0, 1	0, 2	0, 4	0, 2	0, 1

 

М(х²) = 4 0, 1 + 16 0, 2 + 49 0, 4 + 81 0, 2 + 121 0, 1 = 0, 4 + 3, 2 + 19, 6 + 16, 2 +12, 1 = 51, 5

DX = )) – М²(х) = 51, 5 – 6, 7² = 6, 61

= = 2, 57, М_о = 7(р_мах =0, 4).

 

Пример 15. Непрерывная СВ задана функцией распределения

 

F(x) =

Найдите: f(x), МХ, DX, р .

Решение:

f(x) = МХ = ;

 

DX =

 

= = 0, 236; р = F - F 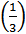= .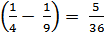