Элементы комбинаторики. .
Для каждого вероятностного эксперимента можно определить пространство элементарных событий. Если это пространство содержит сравнительно небольшое количество событий, то их можно выписать и пересчитать. Если же элементарных событий достаточно много, то для нахождения вероятности нужно вычислить их количество. Комбинаторика – это раздел математики, в котором изучаются методы подсчета количества различных элементов (перестановки, размещения, сочетания). Перестановкой из n элементов называется их произвольный набор. Количество перестановок из n элементов:
Если необходимо выбрать m элементов из n, то следует учитывать состав элементов и в некоторых случаях их порядок. Размещения – это комбинации из n элементов по m, которые отличаются не только составом элементов, но и порядком их следования. Количество размещений из n элементов по m:
Сочетаниями называются такие комбинации из n элементов по m, которые отличаются друг от друга только составом элементов. Общее число сочетаний из n элементов по m обозначается
Пример 2. Рассмотрим различные комбинации чисел 1, 2. 3. Перестановки из чисел 1, 2, 3: {1, 2, 3}, {1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 1, 2}, {3, 2, 1}.
Размещения из чисел 1, 2, 3 по два: {1, 2}, {2, 1}, {1, 3}, {3, 1}, {2, 3}, {3, 2}.
Сочетания из чисел 1, 2, 3 по два: {1, 2}, {1, 3}, {2, 3}.
|
(читается “эн-факториал”)
.
и определяется из формулы: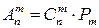
, 
.
.
.
.
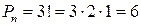