Действия над случайными событиями
Случайные события обозначаются большими латинскими буквами: А, В, С и т.д. Невозможное событие будем обозначать Пусть А и В – некоторые события. 1. Событие С будем называть объединением событий А и В, если С происходит тогда, когда происходит или А, или В. Запись: C = 2. Событие D будем называть пересечением событий А и В, если D происходит тогда, когда происходят А и В одновременно. Запись: D = 3. Событие 4. Событие C называется разностью событий А и В, если С происходит тогда, когда происходит А и не происходит В. Запись: С= Два события являются противоположными, если одно их них происходит тогда, когда не происходит другое (товар реализован – товар не реализован). Пример 1. Бросают игральный кубик. Пусть событие А = {выпадет четное число}, событие В = {выпадет число, которое делится на 3}. Найти сумму, произведение, разность событий А и В, противоположные к ним события. Решение. А = {2, 4, 6}; B = {3, 6}. А + В ={2, 3, 4, 6}. AB = {6}
Иногда случайные события можно записать как объединение некоторых других событий из всего множества возможных событий, например, в примере 1 A = Случайные события, которые нельзя разложить в объединение некоторых других событий, называются элементарными событиями. Таким образом, если мы имеем правильный игральный кубик, то элементарными событиями являются {1}, {2}, {3}, {4}, {5}, {6}.
|
, а множество всех возможных событий – 
.
или С = А + В.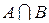
или D = AB.
будем называть дополнением к событию А (противоположным к А), если оно происходит тогда, когда не происходит А. 
.
.
={2, 4}.
={1, 2, 4, 5}.
, где A 1 = {2, 4}, A 2 = {6}.
