Задание 4. Пример 1. Больница специализируется на лечении заболеваний А, Б и В
Пример 1. Больница специализируется на лечении заболеваний А, Б и В. Количества больных, поступающих в эту больницу с заболеваниями А, Б, В, находятся в отношении 5: 3: 2 соответственно. Вероятность полного излечения болезни А равна 0, 7, для болезней Б и В эти вероятности равны соответственно 0, 8 и 0, 9. Найти вероятность того, что поступающий в больницу больной будет выписан здоровым. Решение. Обозначим через
По условию В итоге имеем: Ответ: 0, 77. Пример 2. Решить предыдущую задачу при условии, что требуется найти вероятность того, что выписанный здоровым больной страдал заболеванием В. Решение. Сохраним обозначения, использованные при решении предыдущей задачи. В этих обозначениях требуется найти условную вероятность Ответ:
|

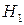 ,
, 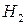 ,
,  соответственно следующие события: «больной страдает болезнью А», «больной страдает болезнью Б», «больной страдает болезнью В». Пусть С – событие «больной будет выписан здоровым». Поскольку
соответственно следующие события: «больной страдает болезнью А», «больной страдает болезнью Б», «больной страдает болезнью В». Пусть С – событие «больной будет выписан здоровым». Поскольку 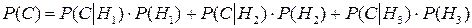 .
. ,
,  ,
,  . Кроме того, поскольку количество больных, А, Б и В, находятся в отношении 5: 3: 2, то
. Кроме того, поскольку количество больных, А, Б и В, находятся в отношении 5: 3: 2, то  ,
,  ,
,  .
. .
. , где событие
, где событие 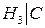 означает «выздоровевший больной страдал болезнью В». Воспользуемся формулой Байеса:
означает «выздоровевший больной страдал болезнью В». Воспользуемся формулой Байеса:  .
. .
.


