Решение. Пусть случайная величина Х выражает число бракованных книг в тиражеПусть случайная величина Х выражает число бракованных книг в тираже. Тогда случайная величина Х распределена по биномиальному закону с параметрами а) Утверждение «тираж содержит не более двух бракованных книг» означает, что бракованных книг может быть 0 (ни одной), 1 или 2. Тогда искомая вероятность будет равна
Эта формула хоть и точная, но трудновычислима. Воспользуемся тем, что поскольку число n велико, а вероятность p мала, случайную величину Х приближенно можно считать распределенной по закону Пуассона с параметром np, т.е.
Ответ: 0, 003. б) Поскольку
Ответ: 0, 997. Пример 2. Длительность Т телефонного разговора является случайной величиной, распределенной по показательному закону. Известно, что средняя длительность телефонного разговора равна 3 минутам. Найти вероятность того, что разговор будет длиться а) не более трех минут; б) более трех минут. Решение. По условию задачи параметр показательного распределения длительности Т равен а) Ответ: 0, 632. б) Ответ: 0, 368.
|
, 
.
.
. В нашем случае 
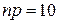. Поэтому искомая вероятность будет приближенно равна
.
, то, используя ранее вычисленное значение, получим
.
.
.
.
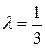