Пример 1. Вероятность попадания в цель для каждого из трех орудий равна соответственно 0, 5; 0, 8; 0, 6. Найти вероятность того, что при залпе из трех орудий
а) все орудия попадут в цель;
б) не попадет в цель ни одно орудие;
в) попадет в цель только одно орудие;
г) попадет в цель хотя бы одно орудие;
д) попадут в цель только два орудия.
Решение.
Обозначим через  событие «i -е орудие при одном выстреле попадает в цель», i = 1, 2, 3. Тогда вероятности этих событий по условию равны:
событие «i -е орудие при одном выстреле попадает в цель», i = 1, 2, 3. Тогда вероятности этих событий по условию равны:
 ,
,  ,
,  .
.
а) Событие  : «все орудия попадут в цель». Три попадания будут тогда и только тогда, когда попадание наступит при каждом выстреле, т.е.
: «все орудия попадут в цель». Три попадания будут тогда и только тогда, когда попадание наступит при каждом выстреле, т.е.  . Тогда по теореме умножения
. Тогда по теореме умножения
 .
.
б) Событие  : «ни одно орудие не попадет в цель». Три промаха будут тогда и только тогда, когда промах явится результатом каждого выстрела, т.е. события
: «ни одно орудие не попадет в цель». Три промаха будут тогда и только тогда, когда промах явится результатом каждого выстрела, т.е. события  осуществляются все вместе:
осуществляются все вместе:  . Тогда по теореме умножения
. Тогда по теореме умножения
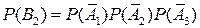 .
.
Учитывая, что
 ,
,
 ,
,
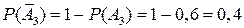 ,
,
получаем
 .
.
в) Событие  : «попадет в цель только одно орудие». При трех выстрелах возможны следующие варианты: первое орудие попадет, второе и третье не попадут; второе попадет, первое и третье не попадут; третье орудие попадет, первое и второе не попадут. Тогда
: «попадет в цель только одно орудие». При трех выстрелах возможны следующие варианты: первое орудие попадет, второе и третье не попадут; второе попадет, первое и третье не попадут; третье орудие попадет, первое и второе не попадут. Тогда  . Поскольку события
. Поскольку события  несовместны, то по теореме сложения
несовместны, то по теореме сложения
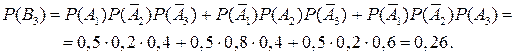
г) Событие 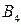 : «попадет в цель хотя бы одно орудие». Это означает, что в цель могут попасть одно, или два, или три орудия, что является противоположным событию «ни одно орудие не попадет в цель», которое рассматривалось в п. б) данной задачи и обозначалось
: «попадет в цель хотя бы одно орудие». Это означает, что в цель могут попасть одно, или два, или три орудия, что является противоположным событию «ни одно орудие не попадет в цель», которое рассматривалось в п. б) данной задачи и обозначалось  . Следовательно,
. Следовательно,  , и
, и
 .
.
д) Событие  : «попадут в цель только два орудия». При трех выстрелах возможны следующие варианты: первое и второе орудие попадут, третье не попадет; первое и третье попадут, второе не попадет; второе и третье попадут, первое не попадет. Тогда
: «попадут в цель только два орудия». При трех выстрелах возможны следующие варианты: первое и второе орудие попадут, третье не попадет; первое и третье попадут, второе не попадет; второе и третье попадут, первое не попадет. Тогда  . Поскольку события
. Поскольку события  несовместны, то по теореме сложения
несовместны, то по теореме сложения


 событие «i -е орудие при одном выстреле попадает в цель», i = 1, 2, 3. Тогда вероятности этих событий по условию равны:
событие «i -е орудие при одном выстреле попадает в цель», i = 1, 2, 3. Тогда вероятности этих событий по условию равны: ,
,  ,
,  .
. : «все орудия попадут в цель». Три попадания будут тогда и только тогда, когда попадание наступит при каждом выстреле, т.е.
: «все орудия попадут в цель». Три попадания будут тогда и только тогда, когда попадание наступит при каждом выстреле, т.е.  . Тогда по теореме умножения
. Тогда по теореме умножения .
. : «ни одно орудие не попадет в цель». Три промаха будут тогда и только тогда, когда промах явится результатом каждого выстрела, т.е. события
: «ни одно орудие не попадет в цель». Три промаха будут тогда и только тогда, когда промах явится результатом каждого выстрела, т.е. события  осуществляются все вместе:
осуществляются все вместе:  . Тогда по теореме умножения
. Тогда по теореме умножения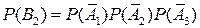 .
. ,
, ,
,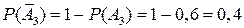 ,
, .
. : «попадет в цель только одно орудие». При трех выстрелах возможны следующие варианты: первое орудие попадет, второе и третье не попадут; второе попадет, первое и третье не попадут; третье орудие попадет, первое и второе не попадут. Тогда
: «попадет в цель только одно орудие». При трех выстрелах возможны следующие варианты: первое орудие попадет, второе и третье не попадут; второе попадет, первое и третье не попадут; третье орудие попадет, первое и второе не попадут. Тогда  . Поскольку события
. Поскольку события  несовместны, то по теореме сложения
несовместны, то по теореме сложения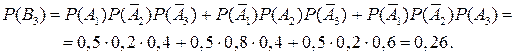
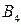 : «попадет в цель хотя бы одно орудие». Это означает, что в цель могут попасть одно, или два, или три орудия, что является противоположным событию «ни одно орудие не попадет в цель», которое рассматривалось в п. б) данной задачи и обозначалось
: «попадет в цель хотя бы одно орудие». Это означает, что в цель могут попасть одно, или два, или три орудия, что является противоположным событию «ни одно орудие не попадет в цель», которое рассматривалось в п. б) данной задачи и обозначалось  , и
, и .
. : «попадут в цель только два орудия». При трех выстрелах возможны следующие варианты: первое и второе орудие попадут, третье не попадет; первое и третье попадут, второе не попадет; второе и третье попадут, первое не попадет. Тогда
: «попадут в цель только два орудия». При трех выстрелах возможны следующие варианты: первое и второе орудие попадут, третье не попадет; первое и третье попадут, второе не попадет; второе и третье попадут, первое не попадет. Тогда  . Поскольку события
. Поскольку события  несовместны, то по теореме сложения
несовместны, то по теореме сложения



