Пусть уравнение 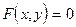 определяет переменную
определяет переменную 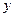 как неявную функцию от переменной
как неявную функцию от переменной 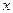 (будем считать эту функцию дифференцируемой). Тогда для нахождения производной
(будем считать эту функцию дифференцируемой). Тогда для нахождения производной  нужно продифференцировать обе части уравнения
нужно продифференцировать обе части уравнения 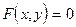 по
по 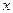 , считая при этом, что
, считая при этом, что 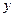 зависит
зависит 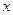 , и из полученного уравнения, линейного относительно
, и из полученного уравнения, линейного относительно  , найти производную.
, найти производную.
Пример 1.
Найти производные функций 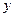 , заданных неявно следующими уравнениями: а)
, заданных неявно следующими уравнениями: а) 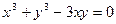 , б)
, б) 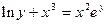 .
.
Решение.
а) Дифференцируем обе части данного уравнения по 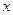 , считая
, считая 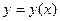 :
:
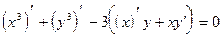
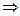
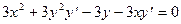 .
.
Слагаемые с 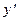 оставляем в левой части равенства, общий множитель
оставляем в левой части равенства, общий множитель 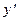 выносим за скобки и находим
выносим за скобки и находим 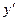 как решение линейного уравнения:
как решение линейного уравнения:
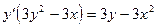
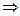
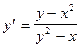 .
.
Производная неявно заданной функции получается выраженной как через аргумент 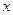 , так и через саму функцию
, так и через саму функцию 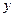 . Поэтому в ответ ее следует записать вместе с уравнением, связывающим
. Поэтому в ответ ее следует записать вместе с уравнением, связывающим 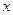 и
и 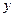 .
.
Ответ: 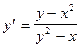 , где
, где 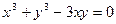 .
.
б) Дифференцируем обе части данного уравнения по 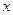 , считая
, считая 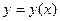 :
:
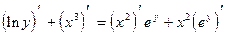
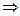
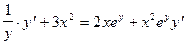 .
.
Слагаемые с 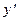 переносим в левую часть равенства, общий множитель
переносим в левую часть равенства, общий множитель 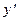 выносим за скобки и решаем уравнение относительно
выносим за скобки и решаем уравнение относительно 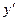 :
:
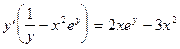
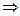
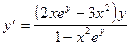 .
.
Ответ: 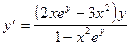 , где
, где 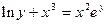 .
.
Если функция 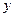 аргумента
аргумента 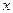 задана параметрически:
задана параметрически:
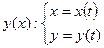 , то ее производная вычисляется по формуле:
, то ее производная вычисляется по формуле: 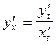 .
.
Пример 2.
Найти производную  функции, заданной параметрически:
функции, заданной параметрически:
а)  , б)
, б)  .
.
Решение.
а) 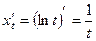 ,
,  .
.
Тогда по формуле 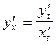 получим
получим 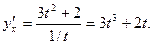
Производная  получилась выраженной через параметр
получилась выраженной через параметр 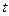 . Как известно, производная функции
. Как известно, производная функции 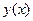 является функцией того же аргумента
является функцией того же аргумента 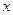 . Поэтому полученная производная в рассматриваемом примере должна быть записана в параметрической форме.
. Поэтому полученная производная в рассматриваемом примере должна быть записана в параметрической форме.
Ответ: 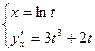 .
.
б) 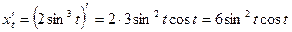 ,
,
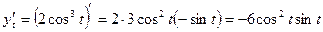 .
.
Тогда по формуле 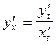 получим
получим 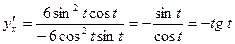 .
.
Ответ: 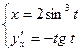 .
.
Самостоятельная работа.
Вариант 1.
а) Найти производную функции 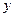 , заданную неявно
, заданную неявно 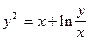 .
.
б) Найти производную  функции, заданной параметрически
функции, заданной параметрически 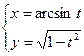 .
.
Вариант 2.
а) Найти производную функции 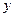 , заданную неявно
, заданную неявно 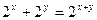 .
.
б) Найти производную  функции, заданной параметрически
функции, заданной параметрически 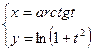 .
.
Вариант 3.
а) Найти производную функции 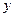 , заданную неявно
, заданную неявно
 .
.
б) Найти производную  функции, заданной параметрически
функции, заданной параметрически
 .
.
Ответы.
Вариант 1.
а) 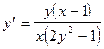 , где
, где 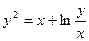 ; б)
; б) 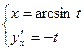 .
.
Вариант 2.
а) 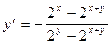 , где
, где 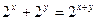 ; б)
; б) 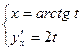 .
.
Вариант 3.
а)  , где
, где  ; б)
; б)  .
.
Дополнительные упражнения.
1. Убедиться в том, что функция 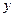 , определяемая уравнением
, определяемая уравнением  , удовлетворяет также соотношению
, удовлетворяет также соотношению 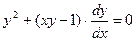 .
.
2. Убедиться в том, что функция 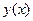 , заданная параметрически уравнениями
, заданная параметрически уравнениями  , удовлетворяет соотношению
, удовлетворяет соотношению 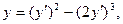 где
где 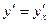 .
.
3. Убедиться в том, что функция 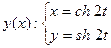 удовлетворяет соотношению
удовлетворяет соотношению 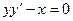 , где
, где 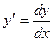 .
.

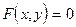 определяет переменную
определяет переменную 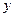 как неявную функцию от переменной
как неявную функцию от переменной 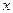 (будем считать эту функцию дифференцируемой). Тогда для нахождения производной
(будем считать эту функцию дифференцируемой). Тогда для нахождения производной  нужно продифференцировать обе части уравнения
нужно продифференцировать обе части уравнения 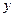 зависит
зависит 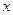 , и из полученного уравнения, линейного относительно
, и из полученного уравнения, линейного относительно 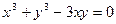 , б)
, б) 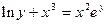 .
.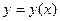 :
: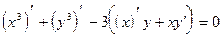
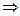
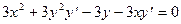 .
.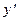 оставляем в левой части равенства, общий множитель
оставляем в левой части равенства, общий множитель 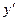 как решение линейного уравнения:
как решение линейного уравнения: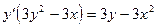
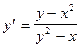 .
.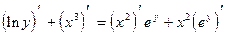
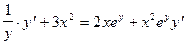 .
.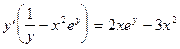
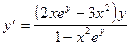 .
.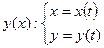 , то ее производная вычисляется по формуле:
, то ее производная вычисляется по формуле: 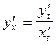 .
. , б)
, б)  .
.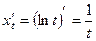 ,
,  .
.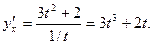
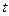 . Как известно, производная функции
. Как известно, производная функции 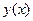 является функцией того же аргумента
является функцией того же аргумента 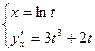 .
.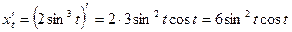 ,
,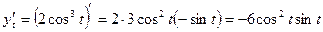 .
.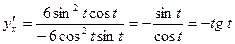 .
.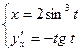 .
.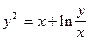 .
.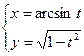 .
.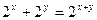 .
.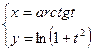 .
. .
. .
.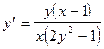 , где
, где 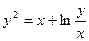 ; б)
; б) 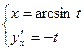 .
.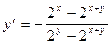 , где
, где 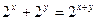 ; б)
; б) 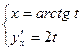 .
. , где
, где  .
. , удовлетворяет также соотношению
, удовлетворяет также соотношению 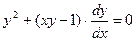 .
. , удовлетворяет соотношению
, удовлетворяет соотношению 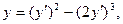 где
где 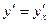 .
.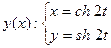 удовлетворяет соотношению
удовлетворяет соотношению 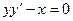 , где
, где 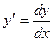 .
.


