Из уравнения первой параболы получаем
Аналогично для второй параболы:
Тогда в точке А(1; 1) Для точки B(4; 4): Тогда Ответ:
Мгновенной скоростью или скоростью изменения функции
Таким образом, производная есть скорость изменения функции.
Пример 5. По оси ОХ движутся две материальные точки, законы движения которых Решение. Найдем скорости обеих точек: Ответ:
Пример 6. Количество электричества Решение. Сила тока I(t) равна мгновенной скорости изменения количества электричества, протекающего через поперечное сечение проводника. Поэтому т.е. сила тока в конце пятой секунды равна 32 амперам. Ответ: 32 амп.
Пример 7. Тело массой (масса Решение. По формуле кинетическая энергия тела Найдем скорость тела через 3с после начала движения:
Значит искомая кинетическая энергия тела равна
Ответ: 36, 75 дж.
Самостоятельная работа. Вариант 1. 1. Записать уравнение касательной и нормали к кривой 2. Материальная точка движется по закону (s - в метрах, t – в секундах). Найти скорость ее движения в момент времени
Вариант 2. 1. Выяснить, в какой точке кривой 2. По оси абсцисс движутся две точки, имеющие законы движения
Вариант 3. 1. В какой точке параболы 2. Радиус шара возрастает равномерно со скоростью 5 см/с. Какова скорость изменения объема шара в момент, когда его радиус становится равным 50 см?
Ответы. Вариант 1. 1. Вариант 2. 1.; 2. 15 м/c. Вариант 3. 1. (2; 0), (0; 6); 2. 0, 05 м3/c.
|

 , тогда
, тогда  .
. ,
,  .
.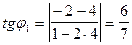
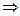
 .
. ,
,  .
.
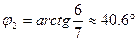 .
. .
. в точке
в точке 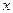 называется
называется .
. и
и  (
( - в секундах). В какой момент времени их скорости окажутся одинаковыми?
- в секундах). В какой момент времени их скорости окажутся одинаковыми? ,
,  . Скорости будут равны при
. Скорости будут равны при  . Решим уравнение
. Решим уравнение  и получим
и получим 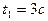 ,
,  .
. (в кулонах), протекающее через поперечное сечение проводника, изменяется по закону
(в кулонах), протекающее через поперечное сечение проводника, изменяется по закону  . Найти силу тока в конце пятой секунды.
. Найти силу тока в конце пятой секунды. и
и  ,
, движется прямолинейно по закону
движется прямолинейно по закону  . Найти кинетическую энергию тела через 3с после начала движения
. Найти кинетическую энергию тела через 3с после начала движения задана в килограммах, путь
задана в килограммах, путь  - в метрах).
- в метрах).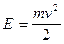 .
.
 .
. (дж).
(дж). в точке
в точке  .
.

 касательная параллельна прямой
касательная параллельна прямой  . Написать уравнение этой касательной.
. Написать уравнение этой касательной. и
и  . С какой скоростью удаляются они друг от друга в момент встречи (х - в метрах, t- в секундах).
. С какой скоростью удаляются они друг от друга в момент встречи (х - в метрах, t- в секундах). следует провести к ней касательную, чтобы последняя проходила через точку М(1; 1)?
следует провести к ней касательную, чтобы последняя проходила через точку М(1; 1)? ; 2.
; 2. 



