Геометрический и механический смысл производной
Если функция
Уравнение касательной к графику функции
Прямая, проходящая через точку Если
Если
Пусть графики функций Угол Если
Пример 1. Под какими углами синусоида Решение. Синусоида Ее производная: Если то есть угловой коэффициент касательной к синусоиде равен единице. Следовательно, в точках Если то есть в этих точках синусоида пересекает ось абсцисс под углом
Ответ:
Пример 2. Написать уравнения касательной и нормали к графику функции Решение. Найдем производную функции:
Вычислим значения функции и ее производной в точке
Запишем уравнение касательной
упрощая которое, получим Запишем уравнение нормали:
упрощая которое, получим Ответ:
|

 имеет производную в точке
имеет производную в точке  , то угловой коэффициент касательной к графику функции в точке
, то угловой коэффициент касательной к графику функции в точке  равен
равен  .
.
 в ее точке
в ее точке  .
. , то уравнение нормали записывается в виде
, то уравнение нормали записывается в виде .
. , то нормаль имеет уравнение
, то нормаль имеет уравнение  .
. пересекаются в точке М 0. За угол
пересекаются в точке М 0. За угол  между графиками этих функций принимается величина меньшего угла, образованного касательными, проведенными к графикам в точке М 0.
между графиками этих функций принимается величина меньшего угла, образованного касательными, проведенными к графикам в точке М 0. ,
,  .
.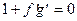 , то
, то  .
. пересекает ось абсцисс?
пересекает ось абсцисс? ,
,  .
.
 , то
, то  ,
, .
. , то
, то  ,
, .
.
 в точке с абсциссой
в точке с абсциссой 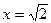 .
.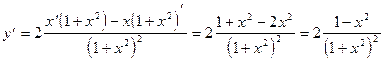 .
. ,
,  .
.
 ,
,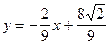
 .
.
 ,
,
 .
. – уравнение нормали.
– уравнение нормали.


