Производные высших порядков. 1.Найти , если .
Пусть функция
Аналогично определяется производная порядка n
при этом под производной нулевого порядка подразумевается сама функция
Пример 1. Найти Решение. Найдем первую производную:
Тогда
Пример 2. Найти Решение. Последовательно находим производные
Пример 3. Записать формулу для производной Решение. Имеем: Заметив закономерность в выражениях для
Пример 4. Найти
Решение. Используем правило однократного дифференцирования функций, заданной параметрически:
Находим первую производную данной в условии задачи функции:
Составляем теперь формулу для второй производной по тому же правилу дифференцирования функции, заданной параметрически:
Вторую производную записываем также в параметрической форме:
Пример 5. Показать, что функция Решение. Находим
Получили верное равенство, значит функция
Самостоятельная работа. Вариант 1. 1. Найти 2. Найти
Вариант 2. 1. Найти 2. Найти
Вариант 3. 1. Найти 2. Найти
Ответы. Вариант 1. 1. Вариант 2. 1. Вариант 3. 1.
Список учебной литературы
1. Пискунов, Н.С. Дифференциальное и интегральное исчисления: Учеб.пособие для вузов: В 2-х т. Т.1/ Н.С. Пискунов. –М.: Интеграл-Пресс, 2001. - 416с.
2. Письменный, Д.Т. Конспект лекций по высшей математике: В 2-х ч. Ч.1/ Д.Т. Письменный. –М.: Рольф, 2001. - 288с.
3. Щипачев, В.С. Высшая математика/ В.С. Щипачев. –М.: Высш.шк., 1988. – 479с.
4. Берман, Г.Н. Сборник задач по курсу математического анализа/ Г.Н.Берман. –М.: Наука, 1985. – 416с.
5. Щипачев, В.С. Сборник задач по высшей математике/ В.С. Щипачев. -М.: Высш.шк., 1998. – 304с.
6. Данко, П.Е. Высшая математика в упражнениях и задачах: В 2-х ч. Ч.1/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. –М.: Высш.шк., 1996. -304с.
|

 дифференцируема на интервале
дифференцируема на интервале  . Производную
. Производную  называют производной первого порядка или первой производной функции
называют производной первого порядка или первой производной функции  ,
, 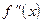 или
или  .
. :
: ,
,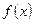 .
. .
.
 .
. .
.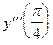 , если
, если  .
. :
:



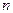 -го порядка, если
-го порядка, если  .
. ,
,  ,
,  .
.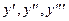 , можно записать формулу для n -й производной
, можно записать формулу для n -й производной  ,
,  .
. для функции, заданной параметрически:
для функции, заданной параметрически: .
. .
.
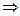
 .
.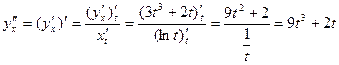 .
. .
. удовлетворяет уравнению
удовлетворяет уравнению  .
.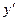 и
и 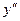 :
: ,
,  , и подставим их в уравнение:
, и подставим их в уравнение:
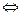
 .
.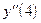 , если
, если  .
. .
. , если
, если  .
. .
. , если
, если  .
.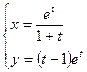 .
. ; 2.
; 2.  .
.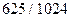 ; 2.
; 2.  .
. ; 2.
; 2.  .
.


